Equivalence in natural deduction in First-order logic

Question

Task

$\vdash \exists x (P(x)\lor Q(x)) \iff \exists xP(x) \lor \exists xQ(x) $

My answer

If we have $A \iff B$ then $A\vdash B$ and $B \vdash A$. So I started trying to see if I could prove $B$ from $A$, but in my tests I couldn't prove that. Below is an image of my attempt.

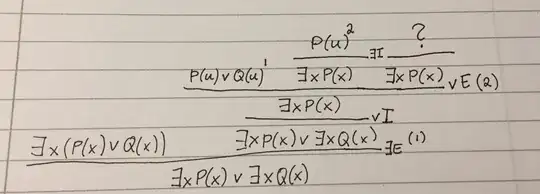
My answer

Is this correct or am I missing a step here? Any help is appreciated, thanks!

Edit

Would it maybe be possible to replace the $?$ with $Q(u) \space\space\space \space \neg Q(u)$ which would result in $\bot$ and from there I could use RAA?

I would start out with an informal "proof in words" that convinces you that the tautology is true. Then, the exercise should become easier, in that you only need to formalize the informal proof. — Daniel Schepler, Aug 20 '18 at 19:02
So my reasoning is that the quantifier "exists" is used the same way on both sides as well as they are using the same domain so they should be equivalent. I'm having a hard time to formulate a "proof in words" because I'm a bit unsure of how to do it when I have a $\lor$ connective. Could you give me some hints? — Fredrik Andersson, Aug 20 '18 at 19:06
Your attempt goes in the wrong direction because as soon as you try to use $\lor_i$ to prove $\exists x P(x) \lor \exists x Q(x)$ without additional hypothesis, you get stuck. See my answer, where I use $\lor_i$ under the additional hypothesis $P(x) \lor Q(x)$. In other words, you should invert the order of the rules $\lor_i$ and $\lor_e$ in your attempt. — Taroccoesbrocco, Aug 20 '18 at 19:29

score 1 · Answer 1 · answered Aug 20 '18 at 19:11

Here's an outline (in words) of how you could approach proving that $LHS \vdash RHS$:

Suppose that $\exists x (P(x) \vee Q(x))$. Then choose a witness $a$ for this existence statement, so that $P(a) \vee Q(a)$. We then proceed using a proof by cases to show that $(\exists x P(x)) \vee (\exists x Q(x))$. In the first case, if $P(a)$, then it immediately follows that $\exists x P(x)$, so we can conclude $(\exists x P(x)) \vee (\exists x Q(x))$. Likewise, if $Q(a)$, then it immediately follows that $\exists x Q(x)$, so we can conclude $(\exists x P(x)) \vee (\exists x Q(x))$ in this case also. $\quad\square$

I think I understand it now, thanks! – Fredrik Andersson Aug 20 '18 at 19:16 — Fredrik Andersson, Aug 20 '18 at 19:16

Taroccoesbrocco · Accepted Answer · 2018-08-20T19:19:47.040

1

A derivation in natural deduction proving that $\exists x (P(x) \lor Q(x)) \vdash \exists x \, P(x) \lor \exists x \, Q(x)$: $$ \dfrac{\exists x (P(x) \lor Q(x)) \quad \dfrac{[P(x) \lor Q(x)]^*\quad \dfrac{\dfrac{[P(x)]^{**}}{\exists y \, P(y)}\exists_i}{\exists y P(y) \lor \exists z Q(z)}\lor_{i_R} \quad \dfrac{\dfrac{[Q(x)]^{**}}{\exists z \, Q(z)}\exists_i}{\exists y P(y) \lor \exists z Q(z)}\lor_{i_L}}{\exists y \, P(y) \lor \exists z \, Q(z)}\lor_e^{**}}{\exists y \, P(y) \lor \exists z \, Q(z)}\exists_e^* $$

The other direction is quite similar: the last rule of the derivation is a $\lor_e$ whose minor premises are conclusions of $\exists_e$.

In both directions there is no need for RAA.

edited Aug 20 '18 at 19:19

answered Aug 20 '18 at 19:15

Taroccoesbrocco

16,964

Thank you once again! – Fredrik Andersson Aug 20 '18 at 19:17
Like this ($B \vdash A$)? I realized that I could have made it even more compact. https://imgur.com/a/wRZ6NF6 – Fredrik Andersson Aug 20 '18 at 19:36
@FredrikAndersson - No, your attempt is wrong because you are violating the constraint about free variables in the rules $\exists_e$ on the top. – Taroccoesbrocco Aug 20 '18 at 19:43
Hmmm, isn't the rule the following? https://imgur.com/a/BSrl9Rb – Fredrik Andersson Aug 20 '18 at 19:52
@FredrikAndersson - Yes but there is a constraint on the free variables of $\psi$. See here for more details and an extensive discussion. – Taroccoesbrocco Aug 20 '18 at 19:58
I'm not sure I follow, u is a free variable that is not bound to the quantifier? So I assume this isn't correct then either? https://imgur.com/a/R4kD5uC – Fredrik Andersson Aug 20 '18 at 20:19
@FredrikAndersson - Yes, your attempt is incorrect because $u$ is a free variable in the conclusion of the rule $\exists_e$, which violate the proviso of the rule $\exists_e$. – Taroccoesbrocco Aug 20 '18 at 20:22
Oh I think I get what you mean now. So this should be correct (sorry for the cramped text)? https://imgur.com/a/ClWrwzf – Fredrik Andersson Aug 20 '18 at 20:30
@FredrikAndersson - Let us continue this discussion in chat. – Taroccoesbrocco Aug 20 '18 at 20:53

Graham Kemp · Answer 3 · 2018-08-21T01:19:22.523

If there is something that satisfies P or Q, then there is a case for something satisfying P or there is a case for something satisfying Q.
$$\dfrac{\dfrac{\dfrac{[\exists x~(P(x)\vee Q(x))]^1}{a:P(a)\vee Q(a)}~\dfrac{\dfrac{[a:P(a)]^2}{\phantom{\exists x~P(x)}}}{\phantom{\exists x~P(x)~\vee~\exists x~Q(x)}}~\dfrac{\dfrac{[a:Q(a)]^2}{\phantom{\exists x~Q(x)}}}{\phantom{\exists x~P(x)~\vee~\exists x~Q(x)}}}{{\exists x~P(x)~\vee~\exists x~Q(x)}}{^2}}{\exists x~(P(x)\vee Q(x))~\to~(\exists x~P(x)~\vee~\exists x~Q(x))}{^1}$$

If there is something that satisfies P then there is something satisfying P or Q. If there is something that satisfies Q then there is something satisfying P or Q. In either case the conclusion holds.

$$\dfrac{\dfrac{\lower{8ex}{[\exists x~P(x)~\vee~\exists x~Q(x)]^1}~\dfrac{[\exists x~P(x)]^2}{\dfrac{\phantom{a:P(a)}}{\dfrac{\phantom{a:P(a)\vee Q(a)}}{\phantom{\exists x~(P(x)\vee Q(x))}}}}~\dfrac{[\exists x~Q(x)]^2}{\dfrac{\phantom{a:Q(a)}}{\dfrac{\phantom{a:P(a)\vee Q(a)}}{\phantom{\exists x~(P(x)\vee Q(x))}}}}}{\exists x~(P(x)\vee Q(x))}{^2}}{(\exists x~P(x)~\vee~\exists x~ Q(x))~\to~\exists x~(P(x)\vee Q(x))}{^1}$$

Equivalence in natural deduction in First-order logic

3 Answers3