Studying a tetrahedron I have identified twelve rotational symmetries and twelve reflectional symmetries. Now I am asked to identify a symmetry that is not a reflection nor a rotation, but which is equal to the product of three reflections.
Label the vertices of your tetrahedron $1,\,2,\,3,\,4$ and consider the reflections $s_1$, $s_2$, and $s_3$ which swap $1\leftrightarrow 2$, $2\leftrightarrow 3$, and $3\leftrightarrow 4$ respectively, and each fix the other vertices. Now their product $t=s_1s_2s_3$ permutes the vertices $1\mapsto 2\mapsto 3\mapsto 4\mapsto 1$, and I claim that this corresponds to a glide reflection of the sphere which circumscribes the tetrahedron. In particular it is neither a reflection nor a rotation. I will give a couple of different ways to think about this.
Realise the tetrahedron as the standard $3$-simplex in $\mathbb{R}^4$, in other words as the convex hull of the points $\{e_1=(1,0,0,0),e_2=(0,1,0,0),e_3=(0,0,1,0),e_4=(0,0,0,1)\}$. Now I am going to perform a change of basis to a new orthonormal basis $$\left\{f_1=\frac{1}{2}(1,1,1,1),f_2=\frac{1}{2}(1,1,-1,-1),f_3=\frac{1}{2}(-1,1,1,-1),f_4=\frac{1}{2}(1,-1,1,-1)\right\}.$$ You can easily check that this is indeed an orthonormal basis. Moreover writing $f_1=(1/2)(e_1+e_2+e_3+e_4)$, etc, it is easy to see that $t(f_1)=f_1$, $t(f_2)=f_3$, $t(f_3)=-f_2$, and $t(f_4)=-f_4$, so writing $t$ as a matrix in the basis $\{f_1,f_2,f_3,f_4\}$ we get $$\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&-1&0&0\\0&0&0&-1\end{pmatrix}$$ In other words $t$ acts trivially on the span of $f_1$, and restricted to the copy of $\mathbb{R}^3$ spanned by the remaining vectors, it is a rotation by $90^\circ$ in the $(f_2,f_3)$-plane, combined with a reflection in that plane, which is orthogonal to $f_4$. Such a rotation-reflection combination corresponds exactly to a glide reflection of the unit sphere in $\mathbb{R}^3$.
Consider the subgroup of the symmetries of the tetrahedron generated by $t$, the action of this group induces on the circumscribing sphere. Note that this action is by isometries.
We can consider the quotient space $\mathbb{S}^2/\langle t\rangle$ under this group action, and it will be different depending on the type of symmetry $t$ is. For example, if $t$ is a reflection, then $\langle t\rangle$ identifies two hemispheres of $\mathbb{S}^2$, and so is just a hemisphere (technically it has the structure of an orbifold but we needn't worry too much about that). On the other hand, if $t$ is a rotation then the quotient space will look like a Rugby (or American foot-)ball
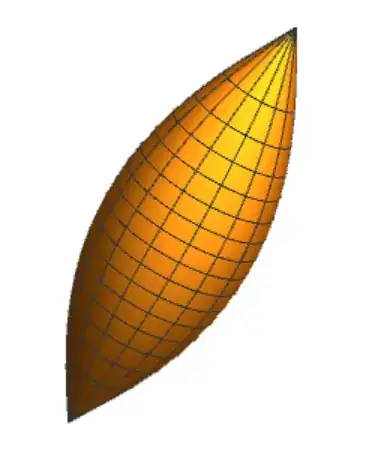
where the cone angles at the two singular points will be equal to the angles of rotation.
What quotient space do we get for $t$ as defined at the top? Well the four faces of the tetrahedron have vertices $\{1,2,3\}$, $\{2,3,4\}$, $\{3,4,1\}$, and $\{4,1,2\}$, so in fact $\langle t\rangle$ acts simply transitively on the faces, so the face $\{1,2,3\}$ (for instance) is a fundamental domain for the action:
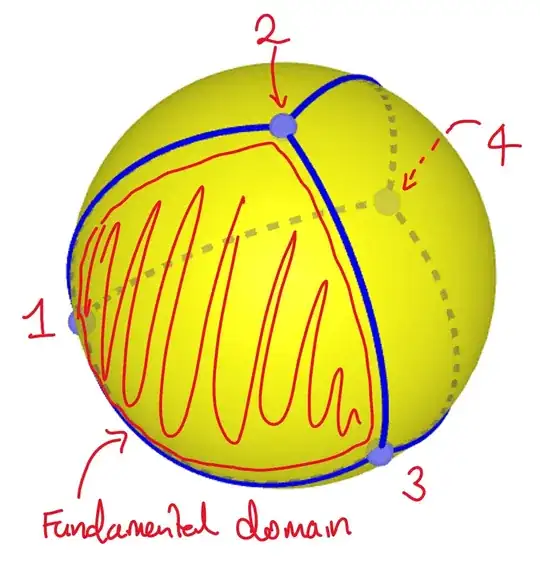
We can form the quotient space by gluing up the boundary of this fundamental domain according to the action of $\langle t\rangle$. I have done this below. Starting with the fundamental domain on the left (which I have drawn flat for illustration), $t$ maps the oriented edge $1\to 2$ to the edge $2\to 3$ (blue gluing arrows), and $t^2$ maps the oriented edge $1\to3$ to $3\to1$ (purple gluing arrows).
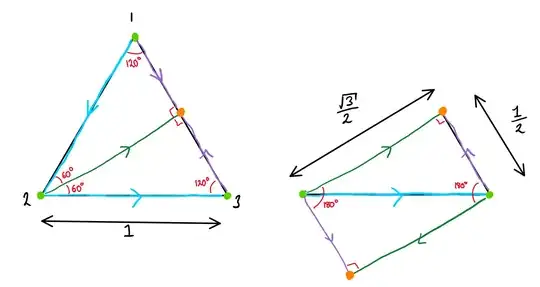
Cutting the fundamental domain along the green line and gluing the blue edges together we form a rectangle there opposite edges are glued with opposite orientations. This means that topologically the resulting quotient space is a projective plane, however keeping track of the spherical angles you can see that the green vertices which get identified have combined the full $360^\circ$, whereas the orange vertices correspond to a cone point with cone angle $180^\circ$. The resulting space looks like this.
This is neither the quotient space for a reflection, nor a rotation. The fact it is a projective plane tells us that $t$ is a glide reflection, and again we can deduce the angle of the rotation component from the cone angle.
