Solve $i^{i^{i^\ldots}}$

Question

How to find $$i^{i^{i^\ldots}} \quad :\quad i=\sqrt{-1}$$ I'm able to find the solution for the finite powers using $$i=e^{i(2k\pi+\frac{\pi}{2})}\quad:\quad k\in\mathbb{Z}$$ $$i^{i}=e^{-(2k\pi+\frac{\pi}{2})}$$ $$i^{i^{i}}=e^{-i(2\pi k+\frac{\pi}{2})}=-i$$ $$i^{i^{i^i}}=e^{(2\pi k+\frac{\pi}{2}) }$$ $$\text{and so on}$$ but what should be the approach to solve for infitie powers$\space$?

Note that one should define exponentiation to be single-valued by choosing a branch, which would make this question clearer... — Simply Beautiful Art, Aug 12 '18 at 03:03
Your method of computing the iterates is not correct. Note that $(i^i)^i \ne i^{(i^i)}$. — shalop, Aug 12 '18 at 03:18
@Shalop What should be the correct method of computing the iterates? — Arpit Yadav, Aug 12 '18 at 03:21
Going by your rules, we say $i^z = e^{\big(2k+\frac12\big)i\pi z}$. Let us call this function $f(z)$. Now compute $f(i)$. Then compute $f(f(i))$. Then compute $f(f(f(i)))$. You will see that it is not the same as what you are doing. — shalop, Aug 12 '18 at 03:44

David G. Stork · Accepted Answer · 2018-08-12T01:49:01.973

4

$X = i^{i^{i^{\cdot}}}$

So $X = i^X$.

So $\log (X) = X \log (i)$.

So ${\log (X) \over X} = \log (i)$.

So $X = i W(-i)$, where $W$ is the Lambert $W$ or PolyLog function.

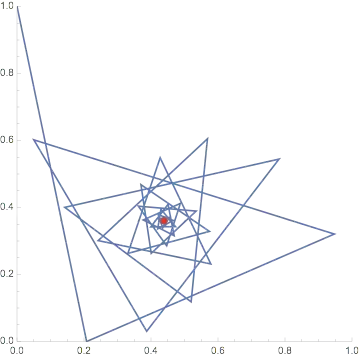
Mathematica evaluates this to $X = 0.44 + 0.36 i$.

Here's a graph on the imaginary plane of 200 successive exponentiations with the solution as a red dot:

edited Aug 12 '18 at 01:49

answered Aug 12 '18 at 01:16

David G. Stork

29,774

5

This is a fixed point but proving that it converges is more work. – parsiad Aug 12 '18 at 01:18
5

@parsiad. Fair enough. Good thing the OP didn't ask for a proof of convergence! – David G. Stork Aug 12 '18 at 01:19
1

@DavidG.Stork Does series converge to any particular value? – Arpit Yadav Aug 12 '18 at 01:21
This is purely formal, obviously. – Did Aug 12 '18 at 03:51

Solve $i^{i^{i^\ldots}}$

1 Answers1