Angle between 2 points and horizontal

Question

I am building trigonometric tables for efficiency. This is for a program, but seeing as programmers can't answer this, I am wondering if you can.

The problem I have encountered is in building a trig table for the arctangent formula. You see, a trig table for sine would look like this:

sin_table[43] -> 0.6819983601...

As you can see, sine of 43 degrees would return 0.6819983601. This is used to increase performance in trig for programs.

Question:

How can I calculate the angle between 2 points and a horizontal without the $\arctan$ function?

Read Before Answering:

$a\cdot b=\|a\|\|b\|\cos\theta$

That will not work. I do not have access to any arc functions, but the other trig functions I do have access to.

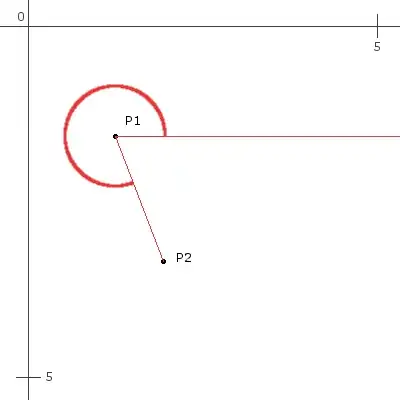
As depicted below, P2 and P1 would be the 2 points, with the angle (Thick red line) goes from the horizontal +x axis, to the line P1P2.

Edit:

I am not trying to build a trig table for the arctan. That would be horribly inefficient and costly on memory. I am just trying to figure out how to calculate it with a function, which should be faster (hopefully) than the bloated existing one. (The pre-existing one can take up to 50 times longer than even complex equations in this language).

Answer 1

When computing functions over an interval,

TAYLOR SERIES ARE BAD!!!!!!!!!!

They are designed to be accurate at a point, and deteriorate away from that point.

Just do a Google search for "Hastings approximation", and you will find this, a link to one of the classic books in the numerical approximation of functions.

This book will show you how to approximate functions, and give you quite useful approximations to many functions, including $\arctan$.

There are other, more recent, collections of approximations, but I remember this one fondly, and have used it often.

Another source for function approximations is the GNU scientific library.

Unless you are required to generate your own function approximation, it is generally far better to use one that someone else has spent the often considerable effort to create.

As to the $\arctan$ approximation blowing up beyond 1, note that $\arctan(1/x) = \pi/2-\arctan(x)$. Also, as noted in Hastings, you can convert an approximation valid over $(-1, 1)$ to one valid over $(0, \infty)$ by $\arctan(x) = \pi/4 + \arctan((x-1)/(x+1))$. This idea of generating an approximation of a function over a limited range and then making an approximation valid over a greater range using the properties of the function is common and extremely useful.

If there is only one word you should know when doing approximations, it is "Chebyshev" (though it has many variant spellings).

Answer 2

Not too well-known, but rather useful in some circumstances, is Borchardt's algorithm, which can be thought of as a modified arithmetic-geometric mean iteration for computing $\arctan\,x$:

$a_0=(1-x)(1+x);\quad b_0=1+x^2;$
$\text{repeat}$
$a_{k+1}=\dfrac{a_k+b_k}{2}$

$b_{k+1}=\sqrt{a_{k+1}b_k}$

$k=k+1$
$\text{until }|a_k-b_k| < \varepsilon$
$\arctan\,x\approx \dfrac{2x}{a_k+b_k}$

(Yes, this is the same algorithm featured in this answer; remember that the logarithm and arctangent are intimately related.)

This of course presumes that you have a square root function available to you. As I mentioned in my other answer, one could choose to accelerate the convergence of this iteration if needed, but there is a storage overhead for this acceleration; if plain Borchardt is not too slow for your needs, then the algorithm given above ought to suffice.

Answer 3

The question you are asking is basically "how can I calculate the arccos function without using arc functions"...

Anyhow, since you are looking to create a trig table for the arctan, I recommend you look at the Taylor or an equivalent series.

$$\arctan(x)=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+...$$

The bad news is that the error in the approximation is about the first missing term. So for example if you only use

$$\arctan(x) \sim x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}$$

the error is about $\frac{x^{11}}{11}$. On computers you can easily keep more terms.

The approximation is very effective for small $x$, for example for $x< \frac{1}{2}$ radians, the first 9 terms approximate the arctan within 4 digits...

And very important, all the computations using this method are done in radians.

Answer 4

If you want a table, you can generate it on a computer that does have inverse trig functions. Excel can make you such a table and store it as a text file, which you can then read in to your program. You could also use your existing tangent table, and interpolate between the points in it. For example, given that $\tan(43^\circ) \approx 0.932515$ and $\tan(44^\circ) \approx 0.965888$, you could determine that $\arctan(0.95) \approx 43+\frac {0.95-0.932515}{0.965888-0.932515}\approx 43.524^\circ$