Drawing and adding marbles to and from a bag

Question

I have a bag with one black marble and one white marble. Whatever color I draw from the bag, I put it back with another marble of the same color. I'm curious about the composition of the bag as I continue playing this game forever. Will it approach a certain ratio asymptotically? If it does, is that ratio highly dependent on the first several draws, or will it always approach the same ratio?

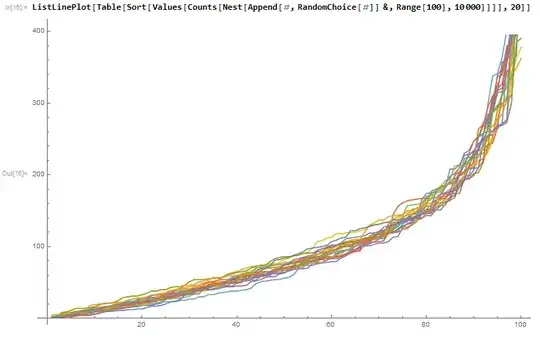
I'm also interested in playing this game with a larger amount of distinct colors to start with. I tried doing just that in Mathematica with a bag starting with 100 colors and applying the procedure 10,000 times. I'd then take the counts of each color, sort them, and plot a graph of the counts from least abundant color to most abundant color. I did it with this line of code:

ListLinePlot[
 Table[Sort[
   Values[Counts[
     Nest[Append[#, RandomChoice[#]] &, Range[100], 10000]]]], 50], 
 PlotRange -> All]

And the graph looks like this

I'd like to learn more about this problem, but I don't have enough experience outside of Calculus to know where to really begin.

For the two-colour version, this is the Polya urn model - there is no limiting ratio though there is a limiting distribution. For muti-colours, it is related to the Dirichlet-multinomial distribution — Henry, Aug 10 '18 at 01:39
Related to https://math.stackexchange.com/questions/378810/a-problem-on-polyas-urn-scheme — saulspatz, Aug 10 '18 at 01:40

score 1 · Answer 1 · answered Aug 10 '18 at 05:27

As mentioned in a comment, this is known as the Pólya urn model; you can find lots of information on it under that name.

The proportion does not approach a certain value, and it does depend strongly on the initial draws. The expected proportion $\lambda_n$ after $n$ draws conditional on any earlier proportion $\lambda_k$ with $k\lt n$ is $\lambda_k$. This is because the expected value of each ball you draw, and thus of each ball you add is $\lambda_k$. In particular, the expected values of all proportions are $\frac12$, but conditional on the first ball drawn they are $\frac13$ or $\frac23$, so the first draw has a great influence.

Drawing and adding marbles to and from a bag

1 Answers1