12

Background. This question originates from the problem of finding a function $f$ such that its $n$-th iterate is equal to its $n$-th power, which I asked about here. Now I would like to focus on the related case $n = -1$, because it seems to be quite a different problem. In other words, I am looking for a function $f$ such that its compositional inverse is equal to its multiplicative inverse, that is, $$f^{-1}(x) = \frac 1 {f(x)}.$$ It is immediate to see that this is equivalent to $$f \left ( \frac 1 {f(x)} \right ) = x$$ which is the equation in the title.

I believe I have found an example of a function $f \colon \mathbb Q^+ \to \mathbb Q^+$ satisfying the equation, but it is quite convoluted. The construction is as follows:

Let $x \in \mathbb Q^+$. Then we can write $$x = \left ( \frac {p_1^{a_1} \dotsb p_h^{a_h}} {q_1^{b_1} \dotsb q_k^{b_k}} \right )^n$$ where $p_1, \dotsc, p_h, q_1, \dotsc, q_k$ are distinct prime factors, $p_1^{a_1} \dotsb p_h^{a_h} \le q_1^{b_1} \dotsb q_k^{b_k}$, the exponents $a_1, \dotsc, a_h, b_1, \dotsc, b_k$ are coprime positive integers, and $n \in \mathbb Z$. Then we define $$\rho \colon \mathbb Q^+ \to \mathbb Q^+ \qquad \rho (x) = \frac {p_1^{a_1} \dotsb p_h^{a_h}} {q_1^{b_1} \dotsb q_k^{b_k}}.$$ Clearly the image $\rho(\mathbb Q^+)$ is countably infinite, so we can fix two sequences $(r_m)_{m \in \mathbb N}$ and $(s_m)_{m \in \mathbb N}$ such that: $$r_0, s_0, r_1, s_1, \dotsc, r_m, s_m, \dotsc$$ is an injective enumeration of $\rho(\mathbb Q^+)$.

Notice then that each $x \in \mathbb Q^+$ is either $r_m^n$ or $s_m^n$ for some $m \in \mathbb N$ and $n \in \mathbb Z$, in a unique way. Therefore, we define $$f(r_m^n) = s_m^n \qquad f(s_m^n) = r_m^{-n}$$ for all $m \in \mathbb N$ and $n \in \mathbb Z$. With this definition, we can check that the above property is satisfied: $$f \left ( \frac 1 {f(r_m^n)} \right ) = f \left ( \frac 1 {s_m^n} \right ) = f (s_m^{-n}) = r_m^n$$ $$f \left ( \frac 1 {f(s_m^n)} \right ) = f \left ( \frac 1 {r_m^{-n}} \right ) = f (r_m^n) = s_m^n.$$

My questions are:

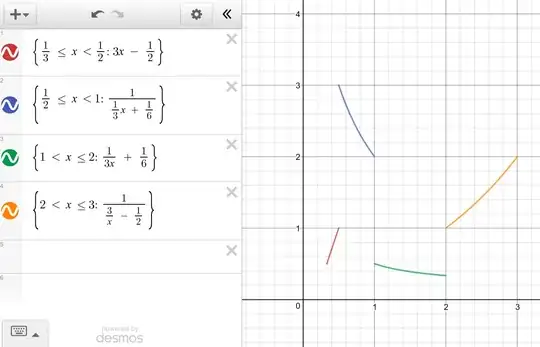
  1. Are there any less artificial functions satisfying the equation?
  2. If so, is there such a function that is defined on an interval of $\mathbb R$?

Remark. If $f$ is defined on an interval $I$ of $\mathbb R$ and is always positive (or negative), then it is monotonic. Indeed, if $f$ were increasing we would have $$x_1 < x_2 \implies f(x_1) < f(x_2) \implies \frac 1 {f(x_1)} > \frac 1 {f(x_2)} \implies x_1 > x_2$$ and similarly if $f$ were decreasing.

Luca Bressan
  • 6,845

2 Answers2

8

(I would put this in a comment but don't have enough reputation.)

The complex function $\frac{z+i}{iz+1}$ seems to satisfy your criterion. There might be a way of making this real?

AdamW
  • 141
  • 4
1

Piecewise examples are possible. For example, we can define $f: [\frac13,3] \to [\frac13,3]$ as follows: $f(1) = 1$, and for all $\frac13 \le x < \frac12$, \begin{align*} f(x) &= 3x - \frac12 &&\in [\tfrac12, 1)\\ f(f(x)) &= \frac1x &&\in(2,3] \\ f(f(f(x))) &= \frac1{3x - \frac12} &&\in(1,2] \\ f(f(f(f(x)) &= x &&\in[\tfrac13,\tfrac12) \end{align*}

Here is a plot: plot

The idea is that we send $[\frac13,\frac12)$ to $[\frac12,1)$ in an increasing manner, then send $[\frac12,1)$ to $(2,3]$, then send $(2,3]$ to $(1,2]$, and finally send $(1,2]$ back to $[\frac13,\frac12)$. It's a 4-cycle.

I'm not sure this example is any less artificial, but it's piecewise continuous (I think being continuous outright is impossible). The example is derived from the following more general necessary and sufficient condition:

Proposition. Assume that $f$'s domain is some set $A \subseteq \mathbb{R}$ which is closed under multiplicative inverse and does not contain $0$. A necessary and sufficient condition for $f$ to satisfy this equation is then that $f(1) = 1$, and that the remaining elements of $A$ are partitioned into quadruples $$ \left\{ a, \frac1a, b, \frac1b \right\}, $$ where $a, b < 1$, $a \ne b$, and $f$ behaves on this set as follows: $f(a) = b$, $f(b) = \frac1a$, $f(\frac1a) = \frac1b$, and $f(\frac1b) = a$.

As a consequence of this, $f(f(f(f(x)))) = x$ for all $x$.

Proof: consider where $f$ maps a pair of elements $\{x, \frac1x\}$, for any $x \ne 1$. Letting $y = f(x)$, we consider the pair $\{y, \frac1y\}$, and notice that $f$ maps $\frac1y$ back to $x$ by the equation $f(1/f(x)) = x$. But then plugging in $\frac1y$ to the equation instead gives that $f$ maps $\frac1x$ to $\frac1y$. Finally, plugging in $\frac1x$ to the equation instead we get that $f$ maps $y$ to $\frac1x$. So $f$ sends $x \mapsto y \mapsto \frac1x \mapsto \frac1y \mapsto x$.

If $x = 1$ or $y = 1$ then this all collapses to $f(1) = 1$. Otherwise, $x, y$ must be distinct, and we get the claim by setting $a$ to be whichever of $x, y, \frac1x, \frac1y$ is smaller than $1$ and maps to something smaller than $1$, and $b$ to whichever of $x, y, \frac1x, \frac1y$ is smaller than $1$ and maps to something larger than $1$.

P.S.: The example in this answer is essentially the same as this answer in the duplicate.

Caleb Stanford
  • 45,895