0

I am trying to calculate total no of sequences possible with given sum k, out of a die (with m outcomes), tossed n times.

I could go after each combination, but $m^n$ grows very large quickly, so want a faster way to generate this. For coin flip, I simply grabbed binomial coefficients of respective row from Pascal's triangle, but here I am stuck on how to proceed. Can you kindly help?

Big picture:I am trying to understand how underlying nature of combinations evolve into normal distribution both theoretically and statistically.

Below is when I throw dice with 3 outcomes (0,1,2), 2 times. I get $[1,2,3,2,1]$ as the frequency of sequence as you see on LHs of the diagram.

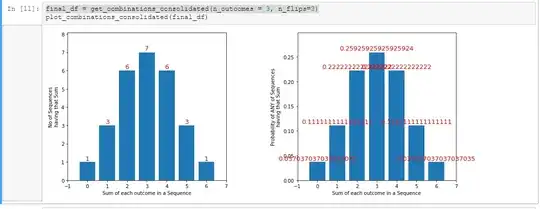
enter image description here

Below is when I throw dice with 3 outcomes (0,1,2), 3 times. I get $[1,3,6,7,6,3,1]$ as frequency of sequence.

enter image description here

I have generated these, by directly generating all possible combinations and counting. When n is large, computing time is exponentially large. So I want a formula shortcut to come up with these frequency values pro grammatically. This is why above question.

Parthiban Rajendran
  • 445
  • here is a discussion of a related problem. – lulu Aug 02 '18 at 11:52
  • checked it, could not relate directly. can you please transform that to this problem? – Parthiban Rajendran Aug 02 '18 at 12:28
  • $a_i$ is the value of the $i^{th}$ die (or one less than that). Your problem is the case where all the $r_i$ are equal. Specifically, if you are dealing with ordinary dice, all of your $r_i$ are $6$. The fact that your rolls are all at least $1$ is not a significant difference, as you can just subtract $n$ from the total and remove that constraint. – lulu Aug 02 '18 at 12:31
  • Worth noting: the first answer specifically addresses the case where all the $r_i$ are equal. – lulu Aug 02 '18 at 12:33
  • Please check if my inference is correct. Suppose I have a die with 3 outcomes (say 0,1,2). I flip it 2 times. Let X be sum of outcomes. I want to calculate $X_2$, that is, how many outcomes where sum is 2. So, $a_1 + a_2 + a_3 = 2$. If so, we need to solve $(1+X+X^2+X^3)^2 = \dfrac {(1-X^4)^2}{(1-X)^2}$? – Parthiban Rajendran Aug 02 '18 at 13:49
  • No. The sum on the left should end at $X^2$. Might be worth noting that, in this specific case, you could just use standard Stars and Bars since the cap is non-restrictive. – lulu Aug 02 '18 at 14:06
  • So it is, $(1+X+X^2)^2 = \dfrac {(1-X^3)^2}{(1-X)^2}$. I will explore Stars and Bars., however how do I solve above equation anyway generically? I am not able to derive further to summation like in that link. – Parthiban Rajendran Aug 02 '18 at 14:12
  • As per Stars and bars here, I should solve for my problem $x_1 + x_2 + x_3 = 2$, so n=2, k =3, so answer should be $\binom {1}{2}$ which would result in negative/complex values? I am missing something. – Parthiban Rajendran Aug 02 '18 at 14:18
  • here is a simple to follow discussion of Stars and Bars. – lulu Aug 02 '18 at 14:30
  • I have updated my question with specific underlying background requirement why I want as well. Please check. I will check wiki and revert. – Parthiban Rajendran Aug 02 '18 at 14:32
  • I tried theorem two also (non negative integers). For die with 2 flips, 3 outcomes, sum needed as 3, it should be $x_1 + x_2 = 3$, so $\binom {n+1}{k-1} = \binom {4}{1} = 4$ But as you can see in my figures above, for $X_k = 3$, the answer should be 2. which are (1,2), (2,1). – Parthiban Rajendran Aug 02 '18 at 14:40
  • Not following. If the possible outcomes are ${0,1,2}$ and you want a sum of $3$ then the cap is restrictive, since combinations like $(0,3)$ are not allowed. – lulu Aug 02 '18 at 14:44
  • In general, details matter. The formulas given in the wiki article are correct. If you are getting different answers it is either because you are asking a different question or because there has been an algebraic error. – lulu Aug 02 '18 at 14:46
  • yeah I am not saying wiki is wrong, but trying to figure out where I am making mistake. – Parthiban Rajendran Aug 02 '18 at 14:47
  • Die with 2 flips, 3 outcomes {0,1,2}, there would be only one sum of 4 which is (2,2). Die with 2 flips, 3 outcomes {0,1,2} there would be only 2 sums of 3 which are (1,2),(2,1). How do I derive this using stars and bars. I am some where making mistake in applying it I guess. – Parthiban Rajendran Aug 02 '18 at 14:49
  • Once again, naive Stars and Bars is only useful if there is no cap. In your first test case, there was no cap (you were asking about a sum of $2$ so the cap of $2$ was already implied). Therefore the method applies. However, if you are asking for a sum of $3$ then the cap does apply so the method does not apply. – lulu Aug 02 '18 at 14:51
  • By cap you mean the limit? If so, in my case, the maximum sum possible out of all outcomes would be the cap. For eg, for die with 2 flips, 3 outcome {0,1,2}, the maximum sum possible is (2,2) = 4, so that is the cap. Kindly enlighten. – Parthiban Rajendran Aug 02 '18 at 14:56
  • Enough. I regret mentioning the standard method, as it has little relevance for the overall problem. It is a powerful tool, but its power is limited here. I suggest studying it further on your own. – lulu Aug 02 '18 at 15:01
  • I tried my best to explain :( – Parthiban Rajendran Aug 02 '18 at 15:03

0 Answers0