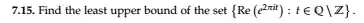-1

A First Course in Complex Analysis by Matthias Beck, Gerald Marchesi, Dennis Pixton, and Lucas Sabalka Exer 7.12,7.15

enter image description here

$$\Re(e^{2 \pi i t}) = \sin(2 \pi t)$$

($\cos$ not $\sin$. nvm. lol.)

enter image description here

(7.12) Where are the errors, if any?

Pf:

$\Leftarrow$

Let $\Re(c_n) \to a, \Im(c_n) \to b$. We must show $c_n$ converges. We can do this by showing it converges to a specific complex number, which we guess is $a + bi$.

We are given that $\forall \varepsilon > 0, \exists N_{\Re},N_{\Im} > 0:$

$$|\Re(c_n) - a| < \frac \varepsilon 2 \Leftarrow n > N_{\Re}$$ $$|\Im(c_n) - b| < \frac \varepsilon 2 \Leftarrow n > N_{\Im}$$

$\therefore, \forall \varepsilon > 0, \exists N > 0:$

$$ |c_n - (a+bi)| = |\Re(c_n)-a + (\Im(c_n)-b)i|$$

$$ \le |\Re(c_n)-a| + |\Im(c_n)-b| < \frac \varepsilon 2 + \frac \varepsilon 2 < \varepsilon \ \text{whenever} \ N := \max\{N_{\Re},N_{\Im}\}.$$

$\Rightarrow$

Let $c_n \to a + bi$. We must show its parts converge. We can do this by showing they converge to specific real numbers which we guess to be $\Re(c_n) \to a, \Im(c_n) \to b$.

We are given that $\forall \varepsilon > 0 \exists N >0:$

$$|c_n-(a+bi)| < \varepsilon \ \text{whenever} \ n > N$$

Observe $$|\Re(c_n)-a|, |\Im(c_n)-b| \le \sqrt{|(\Re(c_n)-a)^2 + (\Im(c_n)-b)^2} = |(\Re(c_n)-a) + i(\Im(c_n)-b)| = |c_n-(a+bi)|$$

$\therefore, \forall \varepsilon > 0, \exists N_{\Re},N_{\Im} > 0:$

$$|\Re(c_n)-a| < \varepsilon \ \text{whenever} \ n > N_{\Re} := N $$ $$|\Im(c_n)-b| < \varepsilon \ \text{whenever} \ n > N_{\Im} := N $$

$\therefore,$ we have shown that:

  • For a convergent complex sequence, we know not only that its parts converge but also their limits: the respective parts of the limit of said convergent complex sequence.

  • Conversely, if a complex sequence's parts converge, then we know not only that the complex sequence converges but also its limit: the complex number whose real part is the limit of the complex sequence's real part and whose imaginary part is the limit of the complex sequence's imaginary part.

This is stronger than the original Exer 7.13.

QED

-

(7.13) Not really complex analysis. Found answer here: How do you prove that Z (the set of integers) equipped with the Euclidean metric (induced from real numbers) is complete?

BCLC
  • 13,459

2 Answers2

1

Assuming you meant $\text { Re } e^{2\pi i t}= \cos(2\pi t),$ note first $\cos(2\pi t)\le 1$ for any real $t,$ so $1$ is an upper bound for the set $E=\{\cos(2\pi t):t\in \mathbb Q\setminus \mathbb Z\}.$ Now let $s < 1.$ Because $\cos(2\pi(1/n)) \to 1$ as $n\to \infty,$ we have $\cos(2\pi(1/n)) >s$ for large $n.$ Thus $s$ is not an upper bound of $E.$ By definition then, $1$ is the least upper bound of $E.$

Your proof of 7.12 is not correct. In fact I can't see what you are trying to do. Let $c_n=x_n+iy_n.$ You are trying to show $c_n$ converges in $\mathbb C$ to $c=x+iy$ iff $x_n\to x$ in $\mathbb R $ and $y_n\to y$ in $\mathbb R .$ This is exactly the same as showing $(x_n,y_n)\to (x,y)$ in $\mathbb R^2$ iff $x_n\to x$ in $\mathbb R $ and $y_n\to y$ in $\mathbb R .$ You must have seen a proof of the latter sometime, somewhere ...

BCLC
  • 13,459
zhw.
  • 105,693
  • Thanks for pointing out cos. I'll try on my own then analyse later – BCLC Aug 05 '18 at 17:50
  • Ayt thanks zhw.! I edited 7.12. Ok now? – BCLC Aug 08 '18 at 05:55
  • 1
    You seem to be showing $c_n=x_n+iy_n \to 0$ in $\mathbb C$ iff $x_n\to 0, y_n\to 0$ in $\mathbb R.$ – zhw. Aug 12 '18 at 15:28
  • LOL THANKS zhw. Edited. Ok now please? – BCLC Aug 13 '18 at 10:15
  • 1
    "Let $\Re(c_n) \to a, \Im(c_n) \to b, c_n \to a + bi$" No, you want to assume $\Re(c_n) \to a, \Im(c_n) \to b,$ and you want to prove $c_n \to a + bi$. Also, starting the proof with " $\forall \varepsilon > 0, \exists N_{\Re},N_{\Im} > 0:$ etc. makes the proof difficult to read. Just let $\epsilon >0.$ – zhw. Aug 13 '18 at 16:58
  • zhw. Thanks. Edited. What do you mean by your last 2 sentences? I mean, what's the difference between $\forall \varepsilon > 0$ and 'Let $\epsilon > 0$' ? – BCLC Aug 14 '18 at 04:27
0

(7.15) $\cos$ not $\sin$.

$1$ would be the sup (and max!) if $\mathbb Q \setminus \mathbb Z$ was replaced with $\mathbb Q$ or $\mathbb Z$. Let's show $1$ still $\sup$ for $\mathbb Q \setminus \mathbb Z$:

  • Obviously, 1 is an upper bound, for $\mathbb Q \setminus \mathbb Z$, $\mathbb Q$ or $\mathbb Z$.

  • Now, we must show that $\forall \varepsilon > 0, \exists t \in [0,1] \cap \mathbb Q \setminus \mathbb Z = (0,1) \cap \mathbb Q: \cos(2 \pi t) \in (1-\varepsilon,1]$. Let us choose $t= \frac{1}{n}, n \ge 2$ where $n$, like $t$, depends on $\varepsilon$:

Observe $\lim \cos(2 \pi \frac 1 n) = 0$, i.e.

$$\forall \varepsilon > 0, \exists N > 0: |\cos(2 \pi \frac 1 n)-1| = 1-\cos(2 \pi \frac 1 n) < \varepsilon \Leftarrow n > N$$

$$\therefore, \forall \varepsilon > 0, \exists N > 0: \cos(2 \pi \frac 1 n) \in (1- \varepsilon, 1] \Leftarrow n > N$$

QED

To recap: For all tolerance levels, we must find some $\cos(2 \pi t), t \in \mathbb Q \cap [0,1]$ s.t. $\cos(2 \pi t) \in (1-\text{tolerance level},1]$. We deduce that for all tolerance levels, we actually have an index $N$ s.t. $$(1-\text{tolerance level},1] \ni \cos(2 \pi \frac 1 {\text{index}+1}), \cos(2 \pi \frac 1 {\text{index}+2}), \cos(2 \pi \frac 1 {\text{index}+3}), \dots $$

So, given a tolerance level, what's our $t$? We have $\infty$ t's: For the same tolerance, these $t$'s work: $$\frac 1 {\text{index}+1}, \frac 1 {\text{index}+2}, \frac 1 {\text{index}+3}, \dots.$$

(7.12) (Edited question, but) To recap:

  • If the real and imaginary parts of $c_n$ (minus, resp, a and b) are kept within a tolerance level by indices $N_R$ and $N_I$, then $c_n-(a+bi)$ is kept within twice of the tolerance level by the maximum of the indices.

  • If $c_n-(a+bi)$ is kept within a tolerance level for a certain index, the same index keeps its real and imaginary parts (minus, resp, a and b) within the same tolerance level.

BCLC
  • 13,459