Langrarian multiplier

Question

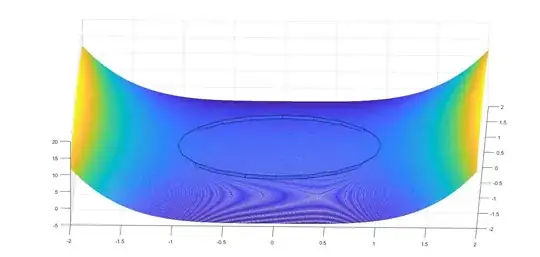
Consider the following function
$$f(x, y)=x^4-y^2$$ And Set $A=\{(x,y)\in R^2: x^2+y^2=1\}$ is required.

find the Lagrangian equation that determines the extreme point of $F$ on $A$ and calculates the solution for this equation.
characterize the above equation into local maxima and minima.
using second order condition explain if there are global maxima and minima.

Welcome to MSE. It will be more likely that you will get an answer if you show us that you made an effort. This should be added to the question rather than in the comments. — José Carlos Santos, Aug 01 '18 at 14:32

score 1 · Answer 1 · answered Aug 01 '18 at 15:13

1

$\nabla (x^4 - y^2) = \nabla(\lambda(x^2+y^2 - 1))$

$4x^3 = 2\lambda x\\ -2y = 2\lambda y$

From the second equation we get: $\lambda = -1 \text { or } y = 0$

if $\lambda = -1\\ 4x^3 = -2x\\ x = 0$

Maxima -- $(1,0),(-1,0)$

Minima -- $(0,1),(0,-1)$

answered Aug 01 '18 at 15:13

Doug M

57,877

score 0 · Answer 2 · answered Aug 01 '18 at 18:32

We know that $$\nabla f=(4x^3,-2y)$$and$$c(x,y)=x^2+y^2-1=0$$therefore the Lagrangian would be $$L(x,y)=\nabla f+\lambda\nabla c=(4x^3,-2y)+\lambda(2x,2y)$$also the Hessian of the function is $$H_f=\begin{bmatrix}12x^2&0\\0&-2\end{bmatrix}$$for finding maxima and minima we have $$4x^3=2\lambda x\\-2y=2\lambda y$$if $y=0$ we have $x=\pm 1$ and $\lambda=2$. The only feasible direction in these points is $\vec d=(0,d_2)$ for any $d_2\in\Bbb R-\{0\}$ from the other side$$dH_f(\pm 1,0)d^T=-2d_2^2<0$$which means that the points $(\pm 1,0)$ are local maxima.

If $\lambda=-1$ we obtain $$4x^3=-2x$$ the only possible candidates are $(0,\pm 1)$ that both are local minima similarly. Here is a sketch:

Langrarian multiplier

2 Answers2