0

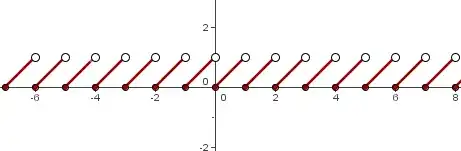
True or false?

The function $$f:[0,10]\to\mathbb R\mid f(x)=x-[x]$$ is Riemann-Integrable.

Here $[x]$ is the floor function, and I think $x-[x]$ is the mantissa function:

Mantissa function

I think the statement is true, but I don't know how to prove in a easy way. Maybe proving that if $f$ is bounded (it's true) then $$\underline{\displaystyle\int_a^bf(x)\;\text dx}\quad=\quad\overline{\displaystyle\int_a^bf(x)\;\text dx}\,,\tag 1$$ but this could be a little tedious?

What are the hypothesis, and my thesis is true? We need to check $(1)$?

Any ideas?

Thank you!

manooooh
  • 2,269
  • 4
    See https://math.stackexchange.com/questions/102844/how-do-i-prove-that-a-function-with-a-finite-number-of-discontinuities-is-rieman? – Robert Z Aug 01 '18 at 09:15
  • Thanks! I am very new with this type of integrals. I will take a look. – manooooh Aug 01 '18 at 09:21
  • 1
    The function considered is a bounded, piecewise continuous function on the interval of integration. The details of the particular function are not necessary to prove its integrability. – Dan Fox Aug 01 '18 at 09:22
  • @DanFox what do you mean by "particular function"? – manooooh Aug 01 '18 at 09:27
  • 2
    @manooooh: I mean it does not matter that you consider $f(x) = x - [x]$. To prove the Riemann integrability, it is enough that the function considered is piecewise continuous and bounded on the interval of integration. In the case of the particular function you consider, it has to be Riemann integrable because just by looking one can calculate the area under its graph ... – Dan Fox Aug 01 '18 at 09:29

1 Answers1

1

If you want to prove this by way of $$ \underline{\displaystyle\int_a^bf(x)\;\text dx}\quad=\quad\overline{\displaystyle\int_a^bf(x)\;\text dx}\,,\tag 1 $$ then it can be done. Take any $\epsilon>0$. We want to make a partition $P = (x_0, x_1, \ldots,x_n)$ of $[0,10]$ (with $x_0 = 0, x_n = 10$, and $x_i<x_{i+1}$) such that $$ U(f, P) - L(f, P)<\epsilon $$ where $U(f, P)$ is the upper sum of $f$ with respect to the partition $P$ and $L(f, P)$ is the lower. It's not too hard to show that any partition where $x_{i+1}-x_i < \epsilon/20$ will work.

Arthur
  • 199,419