22

Consider a random walk of a king on a standard chess board, which at each step moves to a uniformly random permitted square. What's the exact mean time to visit all squares (cover time), starting from a corner square?

Is there an algebraic solution?

mjqxxxx
  • 41,358
Jack
  • 221
  • 1
    Here is a relevant quote from Chapter 12 of Problems and Snapshots from the World of Probability by Blom, Holst, and Sandell. "This problem seems extremely difficult. According to simulation, consisting of one million rounds, the mean is approximately equal to 615." –  Jan 25 '13 at 17:53
  • @Byron: Strangely, the problem is underspecified in the book: "Place a king somewhere on an empty chessboard." From mjqxxxx's results from $597$ to $621$, it seems that the initial position might be meant to be selected at random. – joriki Jan 26 '13 at 11:53
  • @joriki Yes, that makes sense. –  Jan 26 '13 at 15:30
  • What are the asymptotics for the mean time for an nxn board? –  Jan 26 '13 at 19:48

2 Answers2

8

There is in principle no difficulty in answering this question. As I point out in my answer here, calculating the expected cover time of some set $\cal S$ reduces to calculating the expected hitting time of every possible non-empty subset $A$ of $\cal S$:

$$\mathbb{E}(\text{cover time})=\sum_A (-1)^{|A|-1} \mathbb{E}(T_A)$$

These hitting times are defined by $T_A=\inf(n\geq 0: X_n\in A)$.

Look out below! Ignorant of chess rules, I didn't realize that a king can move diagonally. The calculations below are based on a piece that can only move in four ways: north, south, east, or west.

Just to illustrate, let me show you the solution for a $2\times 2$ chessboard:

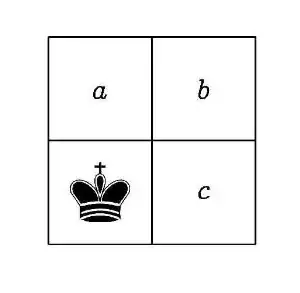
a small board

The expected time to cover the other 3 squares ${a,b,c}$ is equal to $$\mathbb{E}(T_{a})+\mathbb{E}(T_{b})+\mathbb{E}(T_{c})-\mathbb{E}(T_{a,b})-\mathbb{E}(T_{a,c})-\mathbb{E}(T_{b,c})+\mathbb{E}(T_{a,b,c})$$

Standard Markov chain theory uses linear algebra to find these expected hitting times $$\mathbb{E}(T_{a})=\mathbb{E}(T_{c})=3, \mathbb{E}(T_{b})=4, \mathbb{E}(T_{a,b})=\mathbb{E}(T_{b,c})=2, \mathbb{E}(T_{a,c})=\mathbb{E}(T_{a,b,c})=1$$

Putting it all together, we find that the expected cover time is $3+3+4-2-2-1+1=6$.

Note that I counted the king's initial position as already covered. If you require a return to your starting point you can modify the above technique.

The number of terms in the sum make this method impractical for an $8\times 8$ chessboard, however!

Added: If my calculations are correct, the expected cover time for the $3\times 3$ board is $${140803109038245\over 4517710919176}=31.1669$$

Community
  • 1
2

There is an algebraic solution; the mean cover time from any node in a graph is known to be rational and can be found in exponential time. It's not likely to have a simple form, though. Experimentally, I ran the following code:

import random

def reachable((i,j)):
   ok = lambda(q):(min(q)>=1 and max(q)<=8)
   return filter(ok, [(i-1,j-1), (i-1,j), (i-1,j+1), (i,j-1), (i,j+1), (i+1,j-1), (i+1,j), (i+1,j+1)])

def covertime(sq, rng=random.Random()):
   seen = set([sq])
   path = [sq]
   while len(seen)<64:
      path.append(rng.choice(reachable(path[-1])))
      seen.add(path[-1])
   return len(path)-1

I found that the mean cover time starting from a corner square was about $597$, while the mean cover time starting from a center square was larger, about $621$.

mjqxxxx
  • 41,358