If I were asked to "solve" a (monic, integer) quartic polynomial modulo a prime modulus ($23$ in the toy problem described here), I would first determine whether the polynomial can be factored over the rationals (equiv. over the integers by Gauss's lemma).
Here the polynomial turns out to be irreducible over the integers:
$$ f(x) := x^4 + 21x^3 + 5x^2 + 7x + 1 $$
If there were a factor of degree one in $\mathbb Z[x]$, then by the Rational Roots Theorem there would be a root $\pm 1$. It is easily checked that this is not the case. The only other possible factorization over $\mathbb Z[x]$ would be the product of two quadratics:
$$ (x^2 + ax + 1)(x^2 + bx + 1) $$
or:
$$ (x^2 + ax - 1)(x^2 + bx - 1) $$
These possibilities can be ruled out by comparing the coefficients of $x^3$ and $x$ that would result, since this gives inconsistent values of $a+b$.
It is a minor frustration, but if $f(x)$ did factor over the integers, it would also factor over the integers mod $p=23$. The converse is not valid. It often happens that polynomials factor modulo an integer but are irreducible over the rationals (integers).
We now come to a connection with Fermat's Little Theorem:
$$ x^p \equiv x \bmod p $$
for any prime modulus $p$.
Not only are all residues $a = 0,1,\ldots,p-1$ mod $p$ roots of $x^p - x$, this $p$th degree polynomial is the exactly the product of all $p$ of the first degree irreducible polynomials mod $p$. See these class notes (Prop. 1) for a more general proposition for all finite fields.
We proceed to compute the polynomial GCD of $f(x)$ and $x^p - x$, which will give us the product of any first degree factors of $f(x)$. If $f(x)$ splits over the integers mod $p$ (factors completely into first degree polynomials), we would get $\gcd(f(x),x^p-x)=f(x)$ back. That would mean $f(x)$ has four distinct roots without telling us what those are! But in the present case (with two distinct roots), we will instead get $f(x)$ factored as a product of two quadratics mod $p$.
Our chances of getting distinct factors are improved somewhat by noticing how easily factored $x^p - x$ is for odd primes $p$:
$$ x^p - x = x\left(x^{\frac{p-1}{2}} + 1\right)\left(x^{\frac{p-1}{2}} - 1\right) $$
Thus, instead of calculating $\gcd(f(x),x^p-x)$ we can calculate the GCD of $f(x)$ with each of those (coprime) factors of $x^p-x$. This gives a chance of finding a first degree factor in one place and another first degree factor in another place.
By inspection we see that $\gcd(f(x),x) = 1$ because the constant term of $f(x)$ is nonzero. Now with $p=23$ the two interesting factors of $x^p-x$ become $x^{11}+1$ and $x^{11}-1$. We will compute both of their GCD's with $f(x)$, and as it turns out, we will get both of the two distinct first degree factors that way.
Since $x^{11}$ is a "shared" intermediate result, we compute its remainder modulo $f(x)$ and save the effort of doing that twice. It turns out:
$$ x^{11} \equiv 9x^3 - 8x^2 - 2x + 5 \bmod{f(x)} $$
So the first step in finding $\gcd(f(x),x^{11}+1)$ is getting the remainder of $x^{11}+1 \bmod f(x)$ is $9x^3 - 8x^2 - 2x + 6$. Note that we needed to preserve the nonmonic leading term of $x^{11} \bmod f(x)$ because we had to add $+1$ (resp. $-1$) correctly.
However for the follwing steps of the Euclidean algorithm for polynomials it is allowed to factor out that leading coefficient and work only with monic polynomials as the divisors:
$$ 9x^3 - 8x^2 - 2x + 6 \equiv 9(x^3 - 6x^2 + 10x - 7) \bmod 23 $$
Thus the next "division algorithm" step gives us:
$$ f(x) \equiv (x+4)(x^3 - 6x^2 + 10x - 7) - 4x^2 - 3x + 6 \bmod 23 $$
The remainder here becomes our divisor in the next step, so normalizing:
$$ -4x^2 - 3x + 6 \equiv -4(x^2 - 5x + 10) \bmod 23 $$
And so we continue the Euclidean algorithm:
$$ x^3 - 6x^2 + 10x - 7 \equiv (x-1)(x^2 - 5x + 10) - 5x + 3 \bmod 23 $$
$$ -5x + 3 \equiv -5(x+4) \bmod 23 $$
$$ x^2 - 5x + 10 \equiv (x-9)(x+4) + 0 \bmod 23 $$
This last remainder being zero tells us the GCD is found:
$$ \gcd(f(x),x^{11}+1) = x+4 $$
As a first degree factor of $f(x)$, this identifies one of its roots is $-4$ or equivalently modulo $23$, $x=19$.
A similar computation gives $\gcd(f(x),x^{11}-1) = x+5$, which identifies the other roots as $-5$ or $x=18 \bmod 23$.
Because $p=23$ was asked as a "toy problem", I'll point out two ways that computing with a large prime affects the complexity of factoring a quartic polynomial over that field of coefficients. (to be continued)
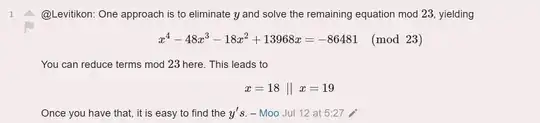
If Euclid is a function that takes in integers
– Levitikon Jul 30 '18 at 23:14aandband returns a single integer that isgcd, how do you get $x^2+9x+20$ from $\gcd(x^4 + 21 x^3 + 5 x^2 + 7 x + 1,x^{23}-x)$? If i'm reading this right, $a = x^4 + 21 x^3 + 5 x^2 + 7 x + 1$ and $b = x^{23}-x$ but they aren't integers to be passed in. Do you use some combination of the exponents or coefficients somehow?