1

I understand from this answer that a Matrix A and its transpose $A^T$ share the same eigenvalues. This is because the transpose operation is commutative, transpose does not change the determinant and we obtain the characteristic polynomial via the determinant.

But I was solving a problem from the ECE GATE 2014 and it seems that A needs to have only real values in order for the eigenvalues to be the same. Since the answer is (b) as eigenvalues of a symmetric matrix can be negative.

Q93

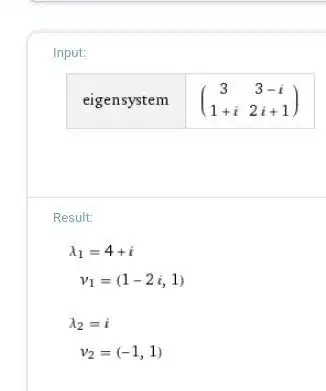
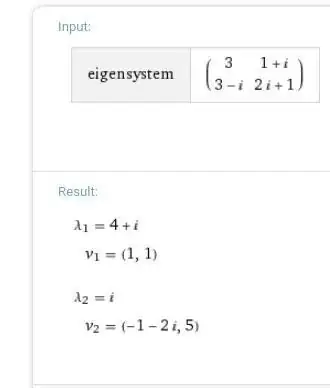
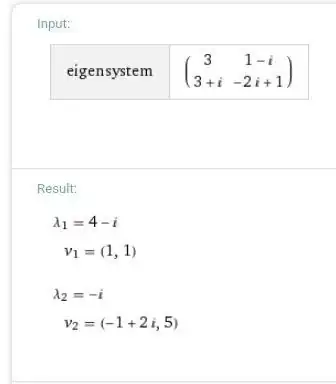
I tried experimenting with different matrices populated with complex values and I find that the eigenvalues are the same.

example

exampleT

Right now I am guessing that when we consider all complex matrices, $A^T$ means A conjugate transpose and not simply transpose. So in the question, they meant $\bar A^T$. In which case,

$$\det(A^{T} - \lambda I) = \det((A - \bar \lambda I)^{T}) = \det (A - \bar \lambda I)$$

So my understanding is that the transpose operation causes the eigenvalues to be conjugated.

My examples also show the same result.

conjugateT

So what is the answer to the GATE question no. 93? Why is (c) not the answer?

José Carlos Santos
  • 427,504
Aditya P
  • 578
  • 7
  • 22
  • 1
    Since $\det A = \det A^T$, you see that $\det (\lambda I -A) = \det (\lambda I -A^T)$. Hence the eigenvalues are the same. No need for $A$ to be real. – copper.hat Jul 26 '18 at 17:14

1 Answers1

3

Because statement (c) is true, as well as statements (a) and (d). Only (b) is false (take $-\operatorname{Id}$, for instance).

And transpose means transpose over whatever field you're working with. Conjugate transpose is another thing.

José Carlos Santos
  • 427,504
  • I mean, why does A have to be real. Why can't A be complex and still $A^T$ seems to have the same eigenvalues. – Aditya P Jul 26 '18 at 16:48
  • 1
    At no point it is written that it has to be real. If, instead of “real”, it was written that the matrix was “rational”, it would still be true. – José Carlos Santos Jul 26 '18 at 16:49
  • So if (c) was "If A is complex, the eigen values of A and $A^T$ are always the same", even then (c) would be true? – Aditya P Jul 26 '18 at 16:51
  • 1
    Yes. And if, instead of complex matrices, we were working with matrices over the field of rational functions in $10$ variables over $\mathbb C$, it would still be true. – José Carlos Santos Jul 26 '18 at 16:54