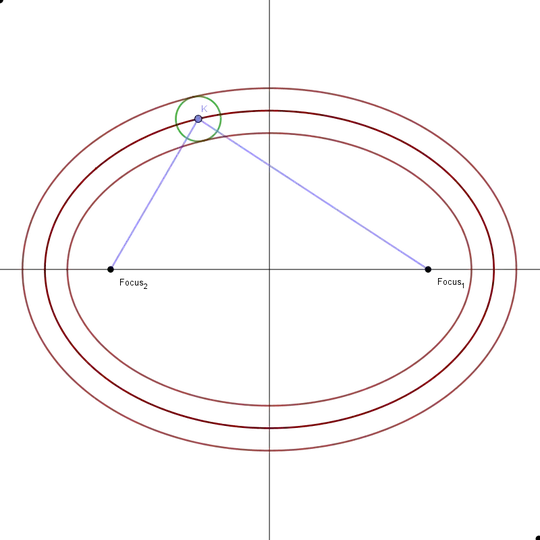
I have created an ellipse of constant thickness. What are the shapes for the inner and outer boundaries? I know they are not also ellipses. I was only able to draw the shape in geometry software, and do not know the formulas. Thanks.
Asked
Active
Viewed 614 times
0
-
Are you looking for a formula (would parametric do?) or a name? Essentially you extend point $K$ by $\pm r$ perpendicularly to the tangent at $K$ – Henry Jul 19 '18 at 22:32
-
1If this previous question similar? The accepted answer describes the constructed curve as a parallel curve. – Weather Vane Jul 19 '18 at 22:48
-
I would like a formula or formulas, yes. I will be working in POV-Ray, so I'm not sure yet whether a parametric function would be better than an implicit function. – posfan12 Jul 19 '18 at 22:50
-
@Weather Vane - Yes that does look like the same question. – posfan12 Jul 19 '18 at 23:00
-
How you define the width - along the vertical or through the origin? – Moti Jul 19 '18 at 23:38
-
May refer to this. – Ng Chung Tak Jul 20 '18 at 09:46
-
See here for a similar question; maybe it gives you ideas: https://math.stackexchange.com/questions/2856323/path-of-a-circle-rolling-on-a-sinewave/2856431#2856431 – Christian Blatter Jul 20 '18 at 09:59
-
Possible duplicate of Uniform thickness border around skewed ellipse? – posfan12 Jul 21 '18 at 04:51
1 Answers
1
The Wikipedia article on Parallel curve has some formulas. It also writes
the offsets of an ellipse or of a hyperbola are not rational
and
an ellipse has as (two-sided) offsets an algebraic curve of degree 8.
So this is going to be a pretty ugly beast of a curve, algebraically speaking, but you can probably use the parametric equation from Wikipedia for some application. As far as names go, “parallel curve to an ellipse” is likely to be as easy as it gets.
MvG
- 42,596