5

I wish to show that the polynomial $f(x)=x^{9}+3x^{6}+165x^{3}+1\in\mathbb{Q}[x]$ is irreducible over $\mathbb{Q}$.

My guess; reducing $f(x)\in\mathbb{F}_{p}[x]$ for suitable prime $p$, it might be irreducible over $\mathbb{F}_{p}$, where $\mathbb{F}_{p}$ is finite field of order $p$.

But, how to find the suitable prime $p$, and to show irreducibility over $\mathbb{F}_{p}$?

The order of $f(x)$ is too much high for me ;(

Give some hint or advice! Thank you!

AnonyMath
  • 1,354
  • Given that $3\mid 3$ and $3, 5, 11\mid 165$, I would at least try $p = 3, 5$ or $11$ first, see if anything immediate pops up. – Arthur Jul 19 '18 at 08:24
  • 1
    It is enough to show that $x^3+3x^2+165x+1$ is irreducible, and it is possible to obtain the roots analytically. –  Jul 19 '18 at 08:31
  • 1
    @Yves Daoust, why is that enough? I mean, could you please elaborate on "it is possible to obtain the roots analytically"? – Ennar Jul 19 '18 at 08:42
  • If the roots of the reduced polynomial aren't rational, neither are those of the original. (In fact it suffices that the roots of the reduced aren't perfect cubes, but this is not needed here.) http://www.wolframalpha.com/input/?i=solve+x%5E3%2B3x%5E2%2B165x%2B1%3D0 –  Jul 19 '18 at 09:15
  • 7
    @YvesDaoust Why would that be enough? There is no general result stating that if $p(x)$ is irreducible, so would $p(x^3)$. Consider $p(x)=x^2+1$. It is irreducible, but $p(x^3)=x^6+1=(x^2+1)(x^4-x^2+1)$. – Jyrki Lahtonen Jul 19 '18 at 10:33
  • @JyrkiLahtonen: you are right. –  Jul 19 '18 at 10:38
  • I just noticed that $\alpha=\root3\of2-\root3\of3$ is one of the zeros. Not unexpectedly it generates a degree nine extension of the rationals. See WimC's follow up question for an explanation. – Jyrki Lahtonen Jul 30 '18 at 21:18

3 Answers3

6

An argument somewhat inspired by pisco's nice answer. Trying to get away with less theory.

Consider the polynomial $$g(x)=x^3+3x^2+165x+1.$$ Let's factor $g(x)\equiv x^3+3x^2-4x+1$ modulo $p=13$. By regrouping we see that $$ g(x)\equiv x^3+3x^2-4x-12=(x^3-4x)+3(x^2-4)=(x-2)(x+2)(x+3). $$ This means that modulo $13$ $$ f(x)\equiv (x^3+2)(x^3-2)(x^3+3).\qquad(*) $$ Pisco already observed that $2$ is not a cubic residue modulo $13$. More generally, because $13-1=3\cdot4$, the (non-zero) residue class of $a$ is a cubic residue modulo $13$ if and only if $a^4\equiv1\pmod{13}$. From this it follows easily that none of $\pm2,-3$ is a cubic reside modulo $13$.

It follows that the three cubic factors in $(*)$ are all irreducible modulo $13$.

The rest is easy. If $f(x)$ factors over $\Bbb{Q}$, it must factor over $\Bbb{Z}$ (Gauss' Lemma), i.e. $f(x)=g(x)h(x)$ with $g(x),h(x)\in\Bbb{Z}[x]$ both monic. Such a factorization survives reduction modulo $13$. Factorization over $\Bbb{Z}_{13}$ is unique, so we can conclude that

  • $g(x)$ and $h(x)$ have degrees $3$ and $6$ (w.l.o.g. we can assume that $g(x)$ is a cubic), and
  • $g(x)$ is congruent to one of the factors in $(*)$ modulo $13$.
  • It follows that the constant term of $g(x)$ is thus congruent to one of $-3,-2,2$ modulo $13$.

This is a contradiction, because the constant term of $g(x)$ must be a factor of the constant term of $f(x)$, i.e. we should have $g(0)=\pm1$.

Therefore $f(x)$ is irreducible.

Addendum: In case it interests someone I did a bit of testing with Mathematica. I collected data on the factorization types of $f(x)$ modulo $1800$ smallest primes not dividing the discriminant (so leaving out $2,3$ and $5$, i.e. multiple factors).

  • Modulo 804 tested primes we get a factorization as a product of three cubics.
  • Modulo 909 tested primes we get a factorization with a single linear and four quadratic factors.
  • Modulo 87 tested primes we get a full factorization with nine linear factors.

In other words, the frequencies follow approximately the $8:9:1$ ratio. Keep in mind that the relative frequency of full splitting is $1/|G|$ and $9\mid |G|$ by irreducibility. Here $G$ is the Galois group of this polynomial.

In light of Dedekind's theorem and Chebotarev's density theorem this strongly (= I will bet a beer saying this is the case) suggests to me that the Galois group of this nonic has order $18$ only. When viewed as a group of permutations of the nine zeros the group has $8$ elements that are products of three disjoint $3$-cycles, and $9$ elements that are products of four disjoint $2$-cycles. Looks an awful lot like $(C_3\times C_3)\rtimes C_2$ with conjugation by the generator of the $C_2$ factor inverting every element of the Sylow $3$-subgroup.

Jyrki Lahtonen
  • 133,153
5

Here is a way using Newton polygons for $f(x-1)$. Specifically $$f(x-1)=x^9-9x^8+36x^7-81x^6+108x^5-81x^4+189x^3-486x^2+486x-162,$$ and looking at the powers of $3$ in its coefficients (the polygon coordinates depends only on these powers, we can ignore signs and other primes), we can write the coefficients as:

$$3^0, 3^2, 3^2, 3^4, 3^3, 3^4, 3^3, 3^5, 3^5, 3^4.$$

The Newton polygon corresponding to $p=3$ is then lower convex hull of points $$[0,4],[1,5],[2,5],[3,3],[4,4],[5,3],[6,4],[7,2],[8,2],[9,0],$$

which can be easily seen to be line segment between $[0,4]$ and $[9,0]$, because all of the points lie above.

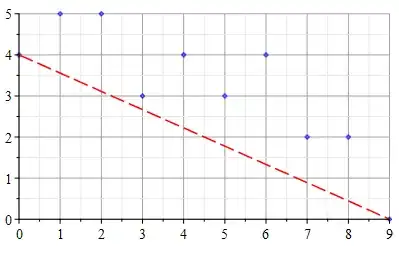
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ enter image description here

We also have $(4,9)=1$ and so this line does not pass through any other integer points. By Dumas' theorem (see for example this Variants of Eisenstein irreducibility, or also Advanced explanation on Eisenstein's criterion), the polynomial $f(x-1)$ is irreducible over $\mathbb{Q}$, and so especially $f(x)$ is irreducible over $\mathbb{Q}$.

Sil
  • 16,612
4

Let $\alpha\in \mathbb{C}$ be any root of $f(x)=x^{9}+3x^{6}+165x^{3}+1$. It is easily seen that $x^3+3x^2+165x+1$ is irreducible. We first show that $[\mathbb{Q}(\alpha):\mathbb{Q}] > 3$.

Let $\beta=\alpha^3$, consider the ring of integers $\mathcal{O}$ of $\mathbb{Q}(\beta)$, the discriminant of $x^3+3x^2+165x+1$ is $-2^2\times 3^{11}\times 5^2$, hence $13$ is relatively prime to the conductor $[\mathcal{O}:\mathbb{Z}[\beta]]$. Since $13\mid f(2)$, there exists a homomorphism: $$\mathcal{O}\to \mathbb{F}_{13}: \beta \mapsto 2$$

If $\alpha\in \mathbb{Q}(\beta)$, then $2$ will be a cubic residue modulo $13$, which is obviously false. Hence $\alpha \notin \mathbb{Q}(\beta)$.

Therefore $$[\mathbb{Q}(\alpha) : \mathbb{Q}(\beta)] > 1 \implies [\mathbb{Q}(\alpha) : \mathbb{Q}] > 3$$

Therefore, we conclude that if $f$ is reducible, then $f$ must be a product of a quartic and quintic. This is easily ruled out, as $[\mathbb{Q}(\alpha) : \mathbb{Q}]$ is a multiple of $3$.

pisco
  • 18,983