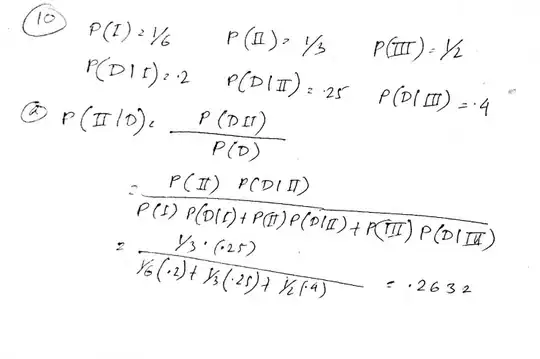0

In the following question, do we assume the probability of selecting each box is 1/3 unless stated otherwise?

  1. There are 3 boxes. First box contains 100 components of which 20 % are defective, second box contains 200 components of which 25 % are defective, third box contains 300 components of which 40 % are defective. Box is selected randomly and from this box one component is selected randomly. The chosen component turned out to be defective. Determine the probability that it came from

a) second box; b)third box.

  1. Urn I has 2 white and 3 blacks balls; urn II, 4 white and 1 black; urn III, 3 white and 4 black. An urn is selected at random and a ball drawn at random is found to be white. Find the probability that urn I was selected.

For the first qt, the solutions say the probability of selecting box 1 is 100/600, box 2 200/600, and box 3 300/600, but that doesnt make sense to me because if the boxes are separate, why would the amount of components matter? If the question said that all the components were scattered into one place and then we select at random, then it would make sense that the probability of selecting from each box wouldn't be 1/3 - ie, the amount of components that were originally in each box would matter. Below is the solution (is it wrong?) for qt 1

enter image description here

David
  • 179
  • 2
    Usually when one says something like "Box is selected randomly" that means uniformly randomly. If the author intended something other than that, it really needed to be spelled out. – lulu Jul 17 '18 at 19:05
  • Possibly helpful: https://math.stackexchange.com/questions/2279851/applied-probability-bayes-theorem/2279888#2279888 – Ethan Bolker Jul 17 '18 at 20:33

2 Answers2

3

I agree to lulu´s comment. I have to admit that I cannot comprehend the provided solution step. My thoughts were the following: For 1. a) and b) you have to use the Bayes theorem. We have the following events:

$D:=$ Detective component is chosen.

$B_i:= $ Box i has been chosen

$$P(B_2|D)=\frac{P(D|B_2)\cdot P(B_2)}{P(D)}$$

For a) the calculation is $$P(B_2|D)=\frac{0.25\cdot \frac13}{P(D)}$$

And using the law of total probability we get

$P(D)=P(B_1)\cdot P(D|B_1)+P(B_2)\cdot P(D|B_2)+P(B_3)\cdot P(D|B_3)$

$=\frac{1}{3}\cdot 0.2+\frac{1}{3}\cdot 0.25+\frac{1}{3}\cdot 0.4$

In total I get $P(B_2|D)=\frac5{17}\approx 29.41\%$

Is it comprehensible ?

callculus42
  • 30,550
  • ok so the probability is 1/3 for each unless otherwise stated right? i dont understand why they did it differently in the solution – David Jul 17 '18 at 20:02
  • @David Yes. If the is no other information we should assume that. It is a miracle for me as well. Does the given solution have another result? If yes, which one? I can only say something serious only if I know the whole calculation of the given solution. But I think they´re on the wrong track. – callculus42 Jul 17 '18 at 20:07
  • I've added the solution to qt 1 in the original post..can you please take a look – David Jul 17 '18 at 20:24
  • @David It can be seen that it is assumed that the probability of selecting box i is not equal for all 3 boxes. But as far as I can see this is not mentioned in the exercise. Usually "selecting randomly" means selecting with equal probability. – callculus42 Jul 17 '18 at 20:31
1

$$P(\text{chosen from the 2nd box}|\text{being defective})=\dfrac{P(\text{chosen from the 2nd box}\cap\text{being defective})}{P(\text{being defective})}=\dfrac{0.25\times \dfrac{1}{3}}{P(\text{being defective})}$$also $$P(\text{being defective})=\dfrac{1}{3}(.20+.25+.40)=\dfrac{17}{60}$$which leads to $$P(\text{chosen from the 2nd box}|\text{being defective})=\dfrac{5}{17}$$similarly$$P(\text{chosen from the 3rd box}|\text{being defective})={8\over 17}\approx0.470588235$$

b)

$$\Pr(\text{chosen form urn 1}|\text{being white})=\dfrac{14}{57}\approx0.245614035$$

Mostafa Ayaz
  • 31,924
  • if the qt had said all the components were mixed together and then we randomly selected one, then wouldn't the probability of selecting a component that was originally in box 1,2,or 3 change? – David Jul 17 '18 at 20:34
  • Sure it does since the larger box still preserves more weight... – Mostafa Ayaz Jul 17 '18 at 20:37