The interconnection between Hyperbolic functions and Euler's Formula

Question

From Euler's identity one may obtain that, $$\sin x=\dfrac{e^{ix}-e^{-ix}}{2i}$$ $$\cos x=\dfrac{e^{ix}+e^{-ix}}{2}$$

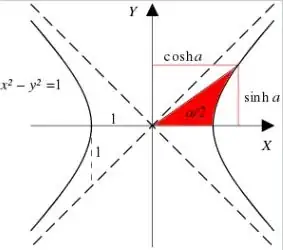
However, it looks quite same to the hyperbolic functions such as $$\sinh x=\dfrac{e^x-e^{-x}}{2}$$ $$\cosh x=\dfrac{e^x+e^{-x}}{2}$$ where the imaginary unit, $i$, is omitted.

Now my question is, what's the interconnection between them? One may answer $\sinh x=-i\sin ix$ or, $\cosh x=\cos ix$ but that doesn't help me to see why it's true. Or even the bigger question what was the necessity to introduce hyperbolic functions? I expect you to help me with this.

P.S. I'm in college. I am seeking for intuition rather than tons of formal theorem.

Answer 1

Just plug the argument $ix$:

$$\sin ix=\frac{e^{i(ix)}-e^{-i(ix)}}{2i}=\frac{e^{-x}-e^{x}}{2i}=i\sinh x.$$

---

The trigonometric and hyperbolic functions are two specializations of the more general complex exponential

$$e^z=e^{x+iy}$$ that is an essential function in calculus.

If you want an explanation that does not involve complex numbers appear explicitly, a true source of trigonometric and hyperbolic function is found in the differential equations

$$y''+y=0$$ (such as that of the oscillations of the pendulum) and $$y''-y=0$$ (found to explain the shape of the catenary).

But if you are not familiar with these concepts and their usefulness in many branches of mathematics and physics, this explanation might be vain.

Answer 2

Usually trigonometric functions are defined geometrically and algebrically starting from the trigonometric unit circle $x^2+y^2=1$ and the link by Euler formula can be found later by more advanced topics.

Hyperbolic functions are usually defined by the given relations and they are geometrically connected to the hyperbola $x^2-y^2=1$.

Hyperbolic functions "occur in the solutions of many linear differential equations (for example, the equation defining a catenary), of some cubic equations, in calculations of angles and distances in hyperbolic geometry, and of Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity".

Answer 3

The circle $x^2+y^2=1$ can be parameterized by $x=\cos t$ and $y=\sin t$.

The hyperbola $x^2-y^2=1$ can be parameterized by $x=\cosh t$ and $y=\sinh t$.

You can also think about them this way

\begin{align} \cos t + i \sin t &= e^{it} \\ \cos t - i \sin t &= e^{-it} \\ \\ \cosh t + \sinh t &= e^{t} \\ \cosh t - \sinh t &= e^{-t} \\ \end{align}

It is called sinh because it is the hyperbolic equivalent of sine.

It is called cosh because it is the hyperbolic equivalent of cosine.

There is an interesting function, called the Gudermannian function that ties the circular and the hyperbolic functions together without using complex numbers.

Answer 4

There is one difference that arises in solving Euler's identity for standard trigonometric functions and hyperbolic trigonometric functions. The difference is that the imaginary component does not exist in the solution to the hyperbolic trigonometric function.

The intuition is that when you plot $e^{ix}$, the graph oscillates between $1$ and $-1$ per Euler's identity.

However, get rid of the imaginary component and what is left is $e^x$. This is a hyperbola.

Answer 5

To answer your question about the significance of $\cos ix=\cosh x$ -- you've proved that the imaginary axis of the complex function $\cos x$ is entirely real-valued, and is equal to the real function $\cosh x$.

Similarly, $\sin ix=i\sinh x$ means that the imaginary axis of $\sin x$ is entirely imaginary-valued (no real-part) and is equal to $i \sinh x$