What is the simplest way to get Bernoulli numbers?

Question

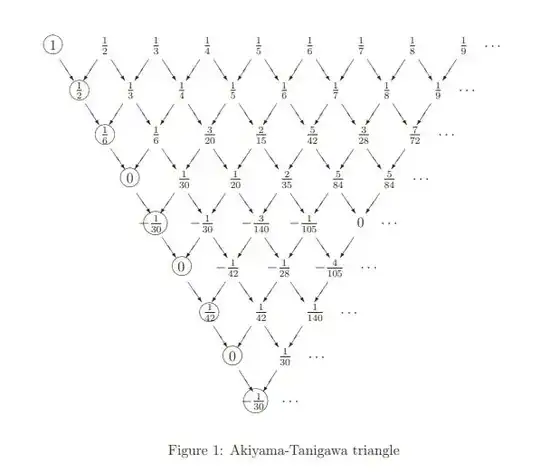
On paper, what is the simplest way to generate the Bernoulli fractions like $\frac{-1}{30} $and $\frac{7}{6}$?

Basically I'm trying to find and understand $B_n =$ (the stuff on this side) and I've seen something using $i$ and a contour integral with

$$\frac{z}{e^z-1}\frac{ dz}{z^{n+1}}$$

and I don't pretend to understand that at all.

$$B_n=\frac{n!}{2\pi \color{red}{i}}\color{red}{\oint}\color{red}{\frac{z}{\color{black}{e\color{red}{^z}}}}\color{red}{\frac{dz}{\color{black}{e^{n+1}}}}$$

$$B_n=\sum^n_{\color{red}{k}=0}\frac{1}{\color{red}{k}+1}\sum^\color{red}{k}_{\color{red}{v}=0}(-1)^\color{red}{v}\color{red}{\binom{k}{v}}\color{red}{v}^n$$

and then there's this variant I see used a lot called a Generating function where

$$B_n = \sum \frac{1}{k+1} \sum (-1)v (k\dots v)v^n$$

but I don't understand double sums either. I need to be able to reliably get Bernoulli numbers for Taylor series stuff like tangent and the hyperbolic variants. I've reached a limit of my understanding and made clear in red the parts I'm confused about. Like I get that the $i$ is imaginary and somehow related to rotation of $\pi$, probably positive and negative, but I don't know what the $d$ or $z$ mean in that equation.

In the second formula, I don't understand why it switched from $n$ to $k$, then from $k$ to $v$, though I suspect I'm supposed to increment $1:1$ increases in $n$ for $k$, which also increases my increments for $v$ by $1:1$ (creating a $\frac{+1}{-1}$ sequence) but I don't understand the vertical parentheses at all. I'm not even going to pretend I took a class above calculus 1.

Answer 1

The simplest way to calculate them, using very few fancy tools, is the following recursive definition:

$$B_n=1-\sum_{k=0}^{n-1}{n\choose k}\frac{B_k}{n-k+1}$$ in other words $$B_n=1-{n\choose 0}\frac{B_0}{n-0+1}-{n\choose 1}\frac{B_1}{n-1+1}-\cdots -{n\choose n-1}\frac{B_{n-1}}{n-(n-1)+1}$$

Here, ${a\choose b}$ denotes a binomial coefficient. So, we begin with $B_0=1, B_1=\frac{1}{2}$, and we can calculate $B_2$ using the above recursive definition. That is, $B_2=1-{2\choose 0}\frac{B_0}{3}-{2\choose 1}\frac{B_1}{2}=1-\frac{1}{3}-2\frac{\frac{1}{2}}{2}=\frac{1}{6}$.

Now, with $B_2$ in hand, we can calculate $B_3$. And so on.

Answer 2

Chowla and Hartung, An "exact" formula for the $n$th Bernoulli number, Acta Arithmetica 22 (1972) 113-115, give the following formula, quoted in Comtet, Advanced Combinatorics: Let $$\phi_n={2(2^{2n}-1)(2n)!\over2^{2n-1}\pi^{2n}}\sum_{k=1}^{3n}k^{-2n}$$ and write $[x]$ for the greatest integer not exceeding $x$. Then $$B_{2n}=(-1)^{n-1}{1+[\phi_n]\over2(2^{2n}-1)}$$

You might also want to look at the paper, Kevin J. McGown, Computing Bernoulli numbers quickly.

My friend, David Harvey, at UNSW, may be the current record holder for fast computation of Bernoulli numbers for large values of $n$. See Richard P. Brent and David Harvey, Fast computation of Bernoulli, Tangent and Secant numbers; see also A multimodular algorithm for computing Bernoulli numbers, Math. Comp. 79 (2010), no. 272, 2361–2370. MR 2684369 (2011h:11019)

Note: I've corrected an error I made in copying the formula out of Comtet.

Answer 3

A straightforward method for generating the Bernoulli numbers is the Akiyama-Tanigawa algorithm.

The algorithm goes like this:

Start with the $0$-th row $1, \frac12, \frac13, \frac14 \ldots$ and define the first row by $$1\cdot(1−\frac12), 2\cdot(\frac12 - \frac13), 3\cdot(\frac13 - \frac14) \ldots$$ which produces the sequence $\frac12, \frac13, \frac14, \cdots$. Then define the next row by $$1\cdot(\frac12 - \frac13), 2\cdot(\frac13-\frac14), 3\cdot(\frac14-\frac15), \ldots$$ thus giving $\frac16, \frac16 \frac3{20}, \ldots $ as the second row. In general, denoting the $m$-th ( $m = 0, 1, 2, \ldots$) number in the $n$-th ($ n = 0, 1, 2, \ldots$) row by $a_{n,m}$, the $m$-th number in the $(n + 1)$-st row $a_{n+1,m}$ is determined recursively by $a_{n+1,m} = (m + 1) \cdot (a_{n,m} − a_{n,m+1})$. Then [...] the $0$-th component $a_{n,0}$ of each row (the “leading diagonal”) is just the $n$-th Bernoulli numbers $B_n$

The algorithm's output looks like:

and produces a value of $B_1 = \frac12$ in accordance with Bernoulli's derivation - the modern standard being $B_1 = -\frac12$.

Answer 4

I sort of favor the $\cot$ Laurent series as a starting point for calculating the Bernoulli numbers. Although the recursive formula still goes over all previous Bernoulli numbers, it includes $2$ per term, so only has half as many terms. If we let $$y(x)=\cot x=\frac1x+\sum_{n=1}^{\infty}\frac{(-1)^nB_{2n}2^{2n}x^{2n-1}}{(2n)!}=\frac1x+\sum_{n=1}^{\infty}a_nx^{2n-1}$$ Then $$\begin{align}y^{\prime}&=-\frac1{x^2}+\sum_{n=1}^{\infty}(2n-1)a_nx^{2n-2}=-\csc^2x=-1-\cot^2x\\ &=-1-y^2=-1-\frac1{x^2}-2\sum_{n=1}^{\infty}a_nx^{2n-2}-\sum_{n=1}^{\infty}\sum_{n=1}^{\infty}a_na_mx^{2n+2m-2}\end{align}$$ So $$\sum_{n=1}^{\infty}(2n+1)a_nx^{2n-2}=\sum_{n=0}^{\infty}(2n+3)a_{n+1}x^{2n}=-1-\sum_{n=1}^{\infty}\left(\sum_{m=1}^{n}a_ma_{n-m+1}\right)x^{2n}$$ Comparing coefficients of like powers of $n$ on both sides we get $$a_1=-\frac13$$ $$a_{2n}=-\frac1{4n+1}\left(a_n^2+2\sum_{m=1}^{n-1}a_ma_{2n-m}\right)$$ $$a_{2n+1}=-\frac2{4n+3}\sum_{m=1}^{n}a_ma_{2n-m+1}$$ Sample program:

program bernoulli
   implicit none
   integer, parameter :: wp = kind(1.0d0)
   integer, parameter :: N = 10
   real(wp) a(N) ! a_n
   real(wp) b(N) ! b_2n
   real(wp) prefactor ! (-1)**n*(2n)!/2**(2n)
   integer i
   prefactor = 1
   do i = 1, N
      if(i == 1) then
         a(1) = real(-1,wp)/3
      else if(mod(i,2) == 0) then
         a(i) = -(a(i/2)**2+2*dot_product(a(1:i/2-1),a(i-1:i/2+1:-1)))/(2*i+1)
      else
         a(i) = -2*dot_product(a(1:i/2),a(i-1:i/2+1:-1))/(2*i+1)
      end if
      prefactor = -2*i*(2*i-1)*prefactor/4
      b(i) = prefactor*a(i)
      write(*,'(*(g0))') 'a(',i,') = ',a(i)
      write(*,'(*(g0))') 'B(',2*i,') = ',b(i)
   end do
end program bernoulli

Output:

a(1) = -.3333333333333333
B(2) = .1666666666666667
a(2) = -.2222222222222222E-01
B(4) = -.3333333333333333E-01
a(3) = -.2116402116402116E-02
B(6) = .2380952380952380E-01
a(4) = -.2116402116402116E-03
B(8) = -.3333333333333333E-01
a(5) = -.2137779915557693E-04
B(10) = .7575757575757573E-01
a(6) = -.2164404280806397E-05
B(12) = -.2531135531135530
a(7) = -.2192594785187377E-06
B(14) = 1.166666666666666
a(8) = -.2221460878997967E-07
B(16) = -7.092156862745096
a(9) = -.2250784651680898E-08
B(18) = 54.97117794486213
a(10) = -.2280515120459217E-09
B(20) = -529.1242424242421