3

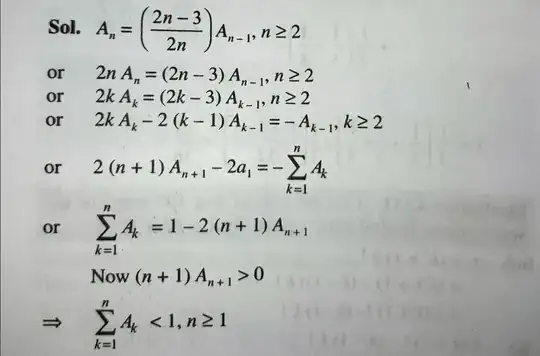
enter image description hereenter image description here I need help with this question. I tried, but couldn't do it. How do I approach it? enter image description here I tried this approach. The problem is, even though it's obvious (by intuition) that the series (A1+A2+A3+......) adds up to less than 1, I can't show it that it does indeed add up to less than 1. Because the series is irregular, without a pattern. How do I prove it? I don't even know if this is the right approach, so please help me with it. Thanks

4d_
  • 570
  • Thoughts: Maybe you can compare it to a geometric sum. You could come up with a geometric sum whose values are close but still bigger to the $A$-terms. – Matti P. Jul 02 '18 at 11:05
  • Thanks, but would it be convincing enough? Good enough, I mean? The series has no pattern. It's not an AP, a GP, or an HP, an AGP... Also, using methods of difference doesn't get us anywhere. I really tried it, but couldn't find a way to add the series. I tried to find a pattern – 4d_ Jul 02 '18 at 11:13
  • Is there any other way I can prove it? – 4d_ Jul 02 '18 at 11:14
  • What I mean is that one way of proving that $$ \sum_{k=1}^n A_k <1 $$ is to find another series, $B_n$ so that $A_n \leq B_n$ and for which it is easy to show that $$ \sum_{k=1}^n B_k <1 $$ So then $$ A_k \leq B_k \Rightarrow \sum_{k=1}^n A_k \leq \sum_{k=1}^n B_k \leq 1 $$ – Matti P. Jul 02 '18 at 11:16
  • Maybe compare $A_k$ to, let's say, $$ B_k = \frac{1}{2^{k+2}} $$ – Matti P. Jul 02 '18 at 11:19
  • How can you compare $A_n$ to a geometric series ??? $\frac{A_n}{A_n-1}\xrightarrow[n\to\infty]{}1$, so $A_n$ will ultimately become larger than any convergent geometric sequence. – Nicolas FRANCOIS Jul 02 '18 at 12:07
  • I don't see anything obvious here. In the limit, $A_n\to A_{n-1}$ and you might as well expect a diverging series. –  Jul 02 '18 at 12:23
  • By simplifying the fractions, you kill the opportunities to find a pattern in the numerators. –  Jul 02 '18 at 12:25
  • I found the solution, but couldn't understand it fully. It makes sense until the 4th step. From fifth step onwards, doesn't quite make sense. Can you explain it please? – 4d_ Jul 02 '18 at 17:12

1 Answers1

1

First you can prove that the sum converges (this step is not necessary, but interesting by itself) : $$\frac{A_n}{A_{n-1}} = 1-\frac{3}{2n}$$ Find a new sequence of the form $B_n=n^{-\alpha}$ such that $\alpha>1$ and $\frac{B_n}{B_{n-1}}>\frac{A_n}{A_{n-1}}$ : $$\frac{B_n}{B_{n-1}} = (\frac{n-1}{n})^\alpha = 1-\frac{\alpha}{n}+o(\frac1n)$$ If you take $\alpha=\frac54$, you can conclude that $\frac{B_n}{B_{n-1}}>\frac{A_n}{A_{n-1}}$ for sufficiently large $n$, which leads to $A_n<B_n$ for $n>N_0$. As $\sum B_n$ converges, so does $\sum A_n$ (this is known as the Raabe-Duhamel criterion in France).

Now note $S_n=\sum_{k=1}^n A_k$. From $2nA_n=(2n-3)A_{n-1}$ follows : $$\sum_{k=1}^n 2kA_k = 2A_1+\sum_{k=2}^n (2k-3)A_{k-1} = 1+\sum_{k=1}^{n-1} (2k-1)A_k = 1 + \sum_{k=1}^{n-1} 2kA_k - S_{n-1}$$ By subtracting the terms present on both side of this last equation, you are down to : $$S_{n-1}=1-2nA_n$$ This by itself is enough to prove $S_n<1$ for all $n$ (the convergence of $\sum A_n$ is useless, it is sufficient to prove that $A_n>0$ for all $n$), but it gives the sum of the series : $$\sum_{k=1}^\infty A_n=1$$ This is because we proved that $A_n<n^{-5/4}$ for sufficiently large $n$.

Nicolas FRANCOIS
  • 4,846