2

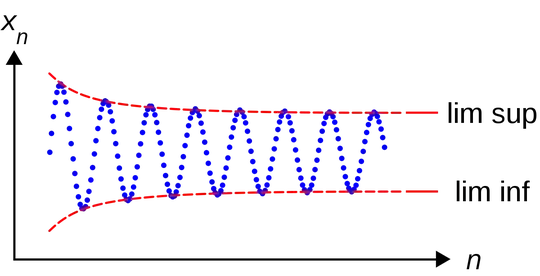
I have trouble understanding the concepts limit superior and inferior using the traditional definition. I have to solve a large problem and I'm not sure of how to do it. I will thank you for any hints or references of books or something where I can find any help:

Exercise 2.6.4. Given a sequence $(x_n)_{n=1}^\infty$ defined in $\mathbb{R}$, number $x^* \in \mathbb{R}$ is said to be its limit superior if $$\forall \varepsilon > 0, \exists n^* \in \mathbb{N} : \forall n > n^* , x_n < x^* + \varepsilon$$ and $$\forall \varepsilon > 0, \forall n \in \mathbb{N}, \exists n_0 > n : x_{n_0} > x^* − \varepsilon.$$ Number $x_* \in \mathbb{R}$ is the sequence’s limit inferior if $$\forall \varepsilon > 0, ∃n_* \in \mathbb{N} : \forall n > n_*, x_n > x_* − \varepsilon$$ and $$\forall \varepsilon > 0, \forall n \in \mathbb{N}, \exists n_0 > n : x_{n_0} < x_* + \varepsilon.$$ When they exist, these numbers are denoted, respectively, as $\operatorname{limsup}_{n\to\infty} x_n = x^*$ and $\operatorname{liminf}_{n\to\infty} x_n = x_*$.

  1. Does the existence of the limit superior of a sequence guarantee that its limit inferior also exists?
  2. Argue that if $\operatorname{limsup}_{n\to \infty} x_n = x^*$, then there exists a subsequence $(x_{n_m})$ of $(x_n)$ that converges to $x^*$.
  3. Argue that, when they both exist, $\operatorname{limsup}_{n\to\infty} x_n \ge \operatorname{liminf}_{n\to\infty} x_n$.
  4. Give an example of a sequence for which the previous inequality is strong.
  5. Argue that if $\lim_{n\to\infty} x_n = x$, then $\operatorname{limsup}_{n\to\infty} x_n = x$.
  6. Argue that if $$\operatorname{limsup}_{n\to\infty} x_n = x = \operatorname{liminf}_{n\to\infty} x_n,$$ then $\lim_{n\to \infty} x_n = x$.
Theo Bendit
  • 50,900
Nathalie Basto Aguirre
  • 21
  • 1
    Please see https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference – Angina Seng Jul 01 '18 at 17:12
  • Limit superior and limit inferior always exists for infinite sequences. It can be $+\infty$ or $-\infty$. – ramanujan Jul 01 '18 at 17:20
  • 1
    My opinion: It's better to define $\limsup x_n$ as the largest subsequential limit of $(x_n).$ I think that's much more intuitive. Same idea for $\liminf x_n$. – zhw. Jul 01 '18 at 17:24
  • 1
    @ramanujan $\pm \infty$ don't really fit into the given definition. – Theo Bendit Jul 01 '18 at 17:44
  • 1
    After you look at Lord Shark's link, I suggest you press "edit" to see how I've formatted your question. Formatting is important; it was nigh unreadable before. – Theo Bendit Jul 01 '18 at 17:47
  • @Theo Bendit yes, this definition allows only finite values. I thought it was equivalent to usual definition. – ramanujan Jul 01 '18 at 17:53
  • @ramanujan I'm not certain what the usual definition is, but as I understand it, to properly formally define it, infinite limits pretty much need to be treated as a separate case anyway (defining some topological concepts first could smooth this out, but nobody does this in a real analysis course!). – Theo Bendit Jul 01 '18 at 17:59
  • @Theo Bendit https://math.stackexchange.com/questions/1710225/can-limit-superior-and-limit-inferior-exist-for-an-unbounded-sequence – ramanujan Jul 01 '18 at 18:03
  • You may have a look at this answer: https://math.stackexchange.com/a/1893725/72031 – Paramanand Singh Jul 02 '18 at 09:33

1 Answers1

2

There are already questions out there which give some equivalent definitions and explanations about $\limsup$ and $\liminf$, for example here.

Personally, I like to think that the sequence eventually becomes "wedged" between the limsup and liminf, as illustrated in the picture below. The picture should give you some good intuition for your questions 2-6.

enter image description here

Sambo
  • 6,243