What is the probability of $m$ random elements generating $S_n$?

Question

Suppose $\{x_k\}_{k=1}^m$ are independent random elements of $S_n$ under discrete uniform distribution. What is the probability $P_m^n$, that $\langle \{x_k\}_{k=1}^m \rangle = S_n$?

It is quite easy to determine $P_m^n$ in several specific cases: For$n \geq 3$ $P_1^n = 0$. $P_m^1 = 1$. $P_m^2 = 1 - \frac{1}{2^m}$. And for any fixed $n$, $\lim_{m \rightarrow \infty} P_m^n = 1$ However, the solution of this problem in general seems to be more complicated.

In general, one can see, that $P_m^n = 1 - Q_m^n$, where $Q_m^n$ is the probability, that $\{x_k\}_{k=1}^m$ all lie in the same maximal subgroup of $S_n$. And here I am stuck, as I do not know the structure of maximal subgroups of $S_n$.

Any help will be appreciated.

Answer 1

For any given $n$, this can be done using Möbius inversion on the lattice of subgroups of $S_n$. For an introduction to Möbius inversion, see e.g. Section $5.2$ of Martin Aigner's A Course in Enumeration. In a nutshell, it's a generalized form of the inclusion–exclusion principle.

I'll work it out for $S_3$ and $S_4$; I don't know of a systematic way of doing it for general $n$.

The subgroup structure of $S_3$ is described here, including this somewhat Enterprise-esque diagram:

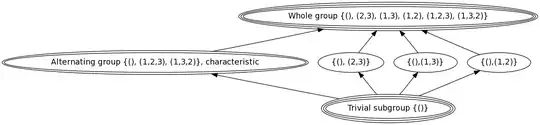
Let's denote the subgroups by $S_3$, $A_3$, $T_1$, $T_2$, $T_3$ and $I$ (from top to bottom and from left to right). Using the superset relation $\supseteq$ as the partial order $\le$, we can find the required values of the Möbius function using Aigner's Proposition $5.4$:

$$\mu(a,a)=1\;,$$

$$ \mu(a,b)=-\sum_{a\le z\lt b}\mu(a,z)\;, $$

and thus

\begin{eqnarray*} \mu(S_3,S_3)&=&1\;,\\ \mu(S_3,A_3)&=&-1\;,\\ \mu(S_3,T_i)&=&-1\;,\\ \mu(S_3,I)&=&3\;. \end{eqnarray*}

If we denote the probability for the subgroup generated by $m$ random elements to be contained in $H$ by $f_m(H)$ and the probability for that subgroup to be exactly $H$ by $g_m(H)$, then

$$ f_m(H)=\sum_{K\subseteq H}g_m(K)\;, $$

so we can use Möbius inversion from above (Aigner's Theorem $5.5$ (ii)) to obtain

$$ g_m(H)=\sum_{K\subseteq H}\mu(H,K)f_m(K) $$

and thus in particular

$$ g_m(S_3)=\sum_{K\subseteq S_3}\mu(S_3,K)f_m(K)\;. $$

With

$$f_m(K)=\left(\frac{|K|}{|S_3|}\right)^m\;,$$

this becomes

$$g_m(S_3)=1-2^{-m}-3\cdot3^{-m}+3\cdot6^{-m}\;.$$

We can check this against a direct calculation for $m=2$, where we have to draw either a transposition and a $3$-cycle or two different transpositions to generate all of $S_3$, with probability

$$ 2\cdot\frac36\cdot\frac26+\frac36\cdot\frac26=\frac12\;, $$

and indeed

$$g_2(S_3)=1-2^{-2}-3\cdot3^{-2}+3\cdot6^{-2}=\frac12\;.$$

The subgroup structure of $S_4$ is analyzed here, including this amazing diagram:

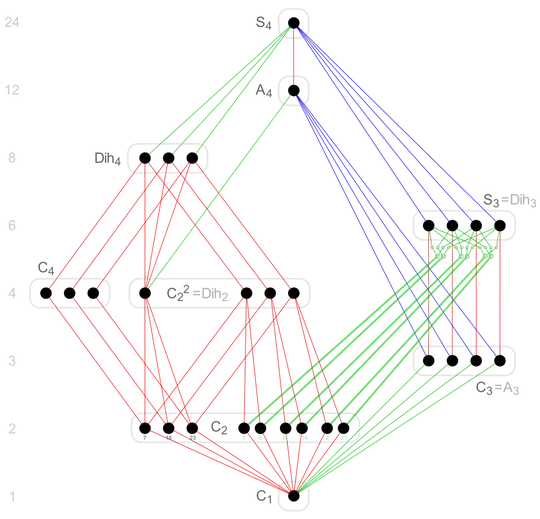
(Attribution for the diagram: By Watchduck (a.k.a. Tilman Piesk) - Own work, CC BY-SA 4.0, Link).

Using the diagram's labels for the types of subgroups (but with $D_4$ instead of $\text{Dih}_4$) and distinguishing the left-hand and right-hand types of $C_2^2$ and $C_2$ groups in the diagram by $L$ and $R$, respectively, we find as above:

\begin{eqnarray*} \mu(S_4,S_4)&=&1\;,\\ \mu(S_4,A_4)&=&-1\;,\\ \mu(S_4,D_4)&=&-1\;,\\ \mu(S_4,S_3)&=&-1\;,\\ \mu(S_4,C_4)&=&0\;,\\ \mu(S_4,C_2^{2L})&=&3\;,\\ \mu(S_4,C_2^{2R})&=&0\;,\\ \mu(S_4,C_3)&=&1\;,\\ \mu(S_4,C_2^L)&=&0\;,\\ \mu(S_4,C_2^R)&=&2\;,\\ \mu(S_4,C_1)&=&-12\;.\\ \end{eqnarray*}

Then Möbius inversion from above yields

$$ g_m(S_4)=1-2^{-m}-3\cdot3^{-m}-4\cdot4^{-m}+3\cdot6^{-m}+4\cdot8^{-m}+12\cdot12^{-m}-12\cdot24^{-m}\;. $$

Again we can check the case $m=2$ by hand. The following pairs of elements of $S_4$ generate all of $S_4$: each one of $6$ transpositions with one of $4$ $3$-cycles or with one of $4$ $4$-cycles, each one of $8$ $3$-cycles with any one of $6$ $4$-cycles, and each one of $6$ $4$-cycles with one of $4$ $4$-cycles, for a probability of

$$ \frac{2\cdot6\cdot4+2\cdot6\cdot4+2\cdot8\cdot6+6\cdot4}{24^2}=\frac38\;, $$

and indeed

$$ g_2(S_4)=1-2^{-2}-3\cdot3^{-2}-4\cdot4^{-2}+3\cdot6^{-2}+4\cdot8^{-2}+12\cdot12^{-2}-12\cdot24^{-2}=\frac38\;. $$

For $m\to\infty$, the leading term will always be the one corresponding to $A_n$, so the probability not to generate all of $S_n$ is asymptotic to $2^{-m}$ for all $n$.

For $m=2$, the problem has been extensively studied; see Probability that two randomly chosen permutations will generate $S_n$. The main result quoted there is the following asymptotic series from John Dixon's paper Asymptotics of generating the symmetric and alternating groups:

$$t_n\sim1-\frac1n-\frac1{n^2}-\frac4{n^3}-\frac{23}{n^4}-\frac{171}{n^5}-\frac{1542}{n^6}+O\left(\frac1{n^7}\right)\;.$$

The numerators form OEIS A113869. This series applies to both the probability that two uniformly randomly chosen elements of $A_n$ generate $A_n$ and the probability that two uniformly randomly chosen elements of $S_n$ generate either $A_n$ or $S_n$; it follows that

$$ g_2(S_n)\sim\frac34t_n\;. $$

The last section of this paper also contains a generalization of this asymptotic series for $m\gt2$.