I am using $\mathbb{N}[i]$ for the Guassian integers that have non-negative real and imaginary components. We can create an ordering on them in the following way : First we will look to magnitude, then we will look to angle. We say that $a+bi<c+di$ when $|a+bi|\leq |c+di|$ and $|a+bi|=|c+di|\implies \tan^{-1}(b/a)<\tan^{-1}(d/c)$.
Consider an "unpairing" function which maps $\mathbb{N}\rightarrow \mathbb{N} [i]$.
$f(n)= x_n+y_ni $ such that $ n < m \implies f(n)<f(m)$. This function is well defined.
$ \begin{align} & f(0)=0 \\ & f(1)=1 \\ & f(2)=i \\ &f(3)=1+i \\ &f(4)=2 \\ &f(5)=2i \\ &f(6)=2+i \\ &f(7)=1+2i \\ \end{align} $
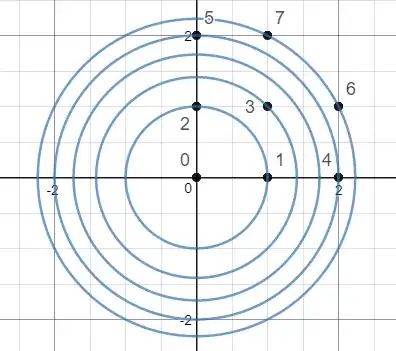
Question:
Is there an explicit formula for $f(n)?$ I can think of an algorithm but not one which is very impressive. I mean: where shall we place $f(1000) =re^{\pi \theta i}$? We know that $r\approx \sqrt{1000}$. But then what's $\theta$? Must we really compute $f(1) \dots f(999)$ to figure this out?
Motivation: I have been thinking about pairing/unpairing functions. It might be useful to have an unpairing function based circles.