Different definitions for submanifolds

Question

I'm trying to better understand the concept of differentiable submanifold. However, it looks like many different definitions are adopted by various authors and so I'm trying to keep myself in sync by proving them equivalent. Now I'm stuck with the following two.

Let $M$ denote a $n$-differentiable manifold and let $M' \subset M$: consider $M'$ equipped with the subspace topology. Also let $n' < n$ be an integer.

I) We say that $M'$ is a $n'$-submanifold of $M$ if it is locally a slice of coordinate system, i.e. for all $p'\in M'$ there exists a coordinate system $(U, x^1 \ldots x^n)$ for $M$ s.t.

$$U \cap M'=\{ p \in M\mid x^{n'+1}(p)=\ldots=x^{n}(p)=0\}.$$

If this is the case $(U \cap M', x^1 \ldots x^{n'})$ is a local chart on $M'$ and the collection of such charts forms a differentiable atlas on it.

II) We say that $M'$ is a $n'$-submanifold of $M$ if for all $p'\in M'$ there exist an open neighborhood $U_{p'}$ of $p'$ in $M$ and a differentiable mapping $\tilde{F}_{p'} \colon U_{p'}\to \mathbb{R}^{n'}$ s.t.:

i) The mapping $F_{p'}=\tilde{F}_{p'}|_{U_{p'} \cap M'}$ is one-one onto an open set $V$ of $\mathbb{R}^{n'}$;

ii) The inverse mapping $F_{p'}^{-1}\colon V \to M$ is differentiable.

If this is the case $(U_{p'}\cap M', F_{p'})$ is a local chart on $M'$ and the collection of such charts forms a differentiable atlas on it.

The difficult part is proving that II $\Rightarrow$ I, that is, given a collection of $(U_{p'}\cap M', F_{p'})$ use them to show that $M'$ is locally a slice of some coordinate system. How do you build a coordinate system like that?

---

Edit: Answer

The following is based on Warner's Foundations of differentiable manifolds and Lie groups, Proposition 1.35. Let $M, M', p', U_{p'}, \tilde{F}_{p'}$ as in II and put $\tilde{F}_{p'}=(y^1\ldots y^{n'})$. Since $F_{p'}$ has a differentiable inverse, the functions $y^1 \ldots y^{n'}$ must be independent at $p'$ and so they form part of a local chart $(W, y=(y^1\ldots y^n))$, where $W$ is an open neighborhood of $p'$ in the big manifold $M$. With no loss of generality let us assume that $y(p')=(0\ldots 0)$.

Now there is no need for the slice $\{p\in W \mid y^{n'+1}(p)=\ldots=y^{n}(p)=0\}$ to agree with $M'$.

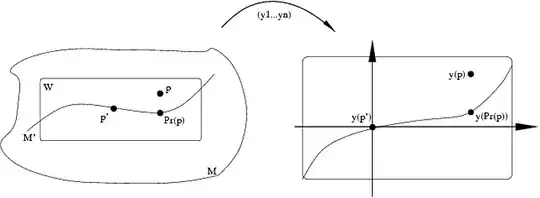
So we need to tweak this coordinate system a little. Define a mapping $Pr\colon W \to W \cap M'$ by setting

$$Pr(p)=(y^1\ldots y^{n'})^{-1} (y^1(p) \ldots y^{n'}(p), 0 \ldots 0).$$

This mapping is best understood in coordinates: $Pr(p)$ is the unique point of $W\cap M'$ whose first $n'$ coordinates agree with the first $n'$ coordinates of $p$. It is clear that this mapping is differentiable (remember hypothesis (ii) above).

Define functions

$$z^i= \begin{cases} y^i & i=1\ldots n' \\ y^i-y^i \circ Pr & i=n'+1 \ldots n \end{cases};$$

those functions are independent at $p'$ and so they form a coordinate system in an open neighborhood $V$ of it. We have $\{p \in V \mid z^{n'+1}(p)=\ldots =z^n(p)=0\}=M' \cap V$: we have thus proven that $M'$ agrees locally with a slice of some coordinate system of $M$, that is, $M'$ verifies I. ////

Answer 1

This is not an answer but a quick observation. Consider $M:=\mathbb{R}^2$ and $M':=\{0\}\times [0,\infty) \cup [0,\infty)\times \{0\}$. Let $\tilde F: (x,y)\mapsto x-y$. Then $F:=\tilde F|_{M'}$ is a bijective mapping $M'\to \mathbb{R}$. This is not a counterexample because (ii) in (II) is not satisfied, but it shows that care has to be taken and (ii) is crucial.

Answer 2

Just going to leave this here as a note to posterity: not all definitions of submanifold are equivalent. So be careful!

For example, Guillemin and Pollack use submanifold to mean "embedded submanifold," whereas Warner uses submanifold to mean "immersed submanifold." These are not equivalent meanings.

Answer 3

From a categorical point of view, the notion of immersed submanifold is probably the best overall definition of a submanifold. This is because it is a kind of 2-subobject, in the sense both the tangent map and the base map are subobjects in the classical categorical sense, that is they are monics and hence injective.

Nevertheless, the other definitions are also useful. One other definition you might not be aware of, is that of initial submanifold, an account is given in Michor, Kolar & Slovak's Natural Operations in Differential Geometry. This definition characterises all initial submanifolds, in the categorical sense, that are also immersed submanifolds.