Proving the product of four consecutive integers, plus one, is a square

Question

I need some help with a Proof:

Let $m\in\mathbb{Z}$. Prove that if $m$ is the product of four consecutive integers, then $m+1$ is a perfect square.

I tried a direct proof where I said:

Assume $m$ is the product of four consecutive integers.
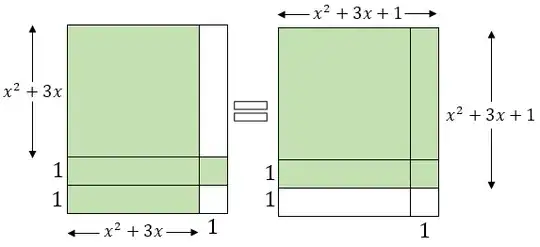
If $m$ is the product of four consecutive integers, then write $m=x(x+1)(x+2)(x+3)$ where $x$ is an integer.
Then $m=x(x+1)(x+2)(x+3)=x^4+6x^3+11x^2 +6x$.
Adding $1$ to both sides gives us:
$m+1=x^4+6x^3+11x^2+6x+1$.

I'm unsure how to proceed. I know I'm supposed to show $m$ is a perfect square, so I should somehow show that $m+1=a^2$ for some $a\in\mathbb{Z}$, but at this point, I can't alter the right hand side of the equation to get anything viable.

Answer 1

By the way, you mean $m+1 = x^4 + 6x^3 + 11x^2 + 6x + 1$.

Let's break it down. Obviously, you need a quadratic that, when squared, gives the above. How do you construct this? You need 3 numbers $a, b, c$ for $ax^2 + bx + c$.

Looking at the 4th degree thing above, what can you tell me about $a$, right off the bat? What about $c$? Then can you use this to tell you what $b$ is?

(I feel like I should not go further because I want you to solve it, but let me know if you need a clarification)

Answer 2

To get a feel for the problem, let's work backwards, starting from a square number. Take some integer $n$.

$n^2 - 1 = (n+1)(n-1).$

OK, so it looks like $m$ has two factors whose difference is 2. Could it be that in our product of consecutive integers, the product of two of them is $n-1$ and of the other two is $n+1$?

Let's throw in a simple example: $1\times2\times3\times4$. Notice how $1\times4=4$ and $2\times3=6$.

What about $2\times3\times4\times5$? This time $2\times5=10$ and $3\times4=12$.

It looks like the product of the "outer" pair is $n-1$ and the product of the "inner pair" is $n+1$.

Now we know how to attack this.

Let $k$ be some integer and $m=k(k+1)(k+2)(k+3)$.

$\begin{align} m &= k(k+1)(k+2)(k+3) \\ &= (k+1)(k+2)\times(k(k+3)) \ \text{ (collecting inner and outer terms)}\\ &= (k^2 + 3k + 2) \times (k^2 + 3k) \\ &= ((k^2 + 3k + 1) + 1) ((k^2 + 3k + 1) - 1) \\ &= (k^2 + 3k + 1) ^ 2 - 1 \qquad \text{ (since }(a+b)(a-b)=a^2-b^2\text{)}. \end{align}$

Since $k$ is an integer, $k^2 + 3k + 1$ is an integer so $m+1$ is a perfect square.

Answer 3

Write the product of the four consecutive integers starting at some $n-1$, so that $$m=(n-1)n(n+1)(n+2)+1,$$ and expand: \begin{align} m&=(n^2-1)(n^2+2n)+1=n^2(n^2-1)+2n(n^2-1)+1 \\ &=(n^2-1)^2+2n(n^2-1)+\not 1+ n^2{-}\!\not1 \\ &= \bigl((n^2-1)+n\bigr)^2. \end{align}

Answer 4

I wrote about this problem at some length on MathEducators StackExchange: MESE 10736.

See Part II there for several approaches taken by students (most of which are covered by other answers here; but the presentation is somewhat different).

One of the methods mentioned there is observing the symmetry above around $x= -3/2 = -1.5$, but then using this to inform a substitution: let $z = x + 1.5$ so that we have:

$$x(x+1)(x+2)(x+3) = (z-1.5)(z-0.5)(z+0.5)(z+1.5) = (z^2 - 1.5^2)(z^2 - 0.5^2)$$

Noting that $1.5^2 = 2.25$ and $0.5^2 = 0.25$, we could use one more substitution of $w = z^2 - 2.25$ to rewrite the final expression above as $w(w+2) = w^2 + 2w$, from which the addition of $1$ yields $(w+1)^2$ as desired. One can now rewrite in terms of just $x$ to finish matters off.

I think that the idea of the symmetry here is an important takeaway; incidentally, the problem is also broached in an exploratory manner at the beginning of Paul Zeitz's (2006) The Art and Craft of Problem Solving as Example 1.2.1.

Answer 5

Given $m$ is the product of four consecutive integers. $$m=p(p+1)(p+2)(p+3)$$where $p$ is an integer

we need to show that $p(p+1)(p+2)(p+3)+1$ is a perfect square

Now,$$p(p+1)(p+2)(p+3)+1=p(p+3)(p+1)(p+2)+1$$ $$=(p^2+3p)(p^2+3p+2)+1$$ $$=(p^2+3p+1)(p^2+3p+2)-(p^2+3p+2)+1$$ $$=(p^2+3p+1)(p^2+3p+1+1)-(p^2+3p+2)+1$$ $$=(p^2+3p+1)(p^2+3p+1)+(p^2+3p+1)-p^2-3p-2+1$$ $$=(p^2+3p+1)(p^2+3p+1)=(p^2+3p+1)^2$$ So, $m+1$ is a perfect square where $m$ is the product of four consecutive integers.

Answer 6

Proof without words:

$\hspace{2cm}$ $$\color{red}x\color{blue}{(x+1)(x+2)}\color{red}{(x+3)}+1=\color{red}{(x^2+3x)}\color{blue}{(x^2+3x+2)}+1=(x^2+3x+1)^2.$$

Answer 7

Note that $f(x)=x(x+1)(x+2)(x+3)+1$ is a degree $4$ polynomial with leading term $x^4$ and symmetric around $x=-\frac32$. We might try the ansatz $f(x)=g(x)^2$ with $g(x)=x^2+px+q$ because then the leading term of $g(x)^2$ is also $x^4$. We suspect that $g$ is also symmetric around $x=-\frac32$ and hence write it as $g(x)=(x+\frac32)^2+c$. Note that $f(0)=f(-1)=1$, so we want $g(0)=\pm1$ and $g(-1)=\pm1$. The first means $c\in\{-\frac54,-\frac{13}4\}$, the second means $c\in\{\frac34,-\frac54\}$. We conclude that $c=-\frac54$. Without further calculation, we see that $f(x)-g(x)^2=0$ for $x=0$ and $x=-1$ and by symmetry also for $x=-2$ and $x=-3$. As the leading terms cancel, the polynomial $f(x)-g(x)^2$ is in fact of degree of at most $3$. Having four distinct roots, it must be identically zero, as desired.

Answer 8

\begin{eqnarray*} m=n(n+1)(n+2)(n+3) =n^4+6n^3+11n^2+6n. \end{eqnarray*} So \begin{eqnarray*} m+ 1 =n^4+6n^3+11n^2+6n+1=(n^2+3n+1)^2. \end{eqnarray*}

Answer 9

The polynomial $x^4+6x^3+11x^2+6x+1$ has symmetric coefficents - more precisely, it's called a palindromic polynomial:

$$p(x)=x^4+ax^3+bx^2+ax+1$$

The goal is to factor $p(x)$ (and show that it factors to a square of some expression). Let's start by dividing by $x^2$ and refactoring:

$$\frac{p(x)}{x^2} = q(x) = x^2+\frac{1}{x^2}+a\left(x+\frac{1}{x}\right)+b$$

It's tempting to make a substitution $y=x+\frac{1}{x}$:

$$q(x) \rightarrow q(y) = y^2+ay+(b-2)$$

This: $q(y)=0$, being a quadratic equation, is something that can be automatically solved:

$$y_{1,2}=\frac{-a\pm \sqrt{a^2-4(b-2)}}{2}$$

and inserting the values $a=6$ and $b=11$, one obtains (note the expression under the square root is equal to zero):

$$y_1=y_2=-3$$

so that $q(y)=(y+3)^2$ - at this point one sees it's a perfect square, and due to $q(y)=\frac{p(x)}{x^2}$, basically we're done with the proof at this point.

---

Just to take things to their end:

Because $q(y)=0 \Leftrightarrow q(x)=0 \Leftrightarrow p(x)=0 $:

$$q(y) = (y+3)^2 = \left(x+\frac{1}{x}+3\right)^2 = \frac{(x^2+3x+1)^2}{x^2} = \frac{p(x)}{x^2}$$

hence $x^4+6x^3+11x^2+6x+1 = (x^2+3x+1)^2$ - a perfect square indeed.

Answer 10

Empirically:

Consider the function

$$p(n):=\sqrt{n(n+1)(n+2)(n+3)+1}.$$

For $n=0,1,2,3,\cdots$ we have $p(n)=1,5,11,19,29,\cdots$ a sequence with constant second order differences ($2$), and we can postulate the polynomial

$$n^2+3n+1$$

(because $p(0)=1$, the coefficient of $n^2$ must be $1$, and $p(n)-n^2-1=0,3,6,9,\cdots$)

Now the identity

$$n(n+3)(n+1)(n+2)=(n^2+3n)(n^2+3n+2) \\=(n^2+3n+1-1)(n^2+3n+1+1) \\=(n^2+3n+1)^2-1.$$

becomes apparent.

---

Another approach is by bringing more symmetry and shifting the variable by $3/2$.

$$\sqrt{\left(m-\frac32\right)\left(m-\frac12\right)\left(m+\frac12\right)\left(m+\frac32\right)+1} =\sqrt{\left(m^2-\frac94\right)\left(m^2-\frac14\right)+1} =\sqrt{m^4-\frac52m^2+\frac{25}{16}}=m^2-\frac54, $$

which is

$$n^2+2\frac32n+\left(\frac32\right)^2-\frac54.$$

Answer 11

If the numbers are $x, x+1, x+2, x+3$.

Let $\frac m2 = x+1.5$ be the midpoint of the four consecutive integers, so that the integers are $\frac {m-3}2, \frac {m-1}2, \frac {m+1}2, \frac {m+3}2$. (Note: $m$ is odd and $\frac m2$ is not an integer.)

So $x(x+1)(x+2)(x+3) + 1 = $

$\frac {(m-3)(m+3)(m-1)(m+1)}{16} + 1=$

$\frac {(m^2 -9)(m^2 - 1) + 16}{16} =$

$\frac {(m^2-10m^2 + 9) +16}{16} =\frac {m^2-10m^2 + 25}{16}=$

$(\frac {m^2 -5}{4})^2$.

Now $m$ is odd. So let $m = 2n+1$ then

$x(x+1)(x+2)(x+3) + 1 = (\frac {(2n+1)^2 -5}{4})^2=$

$(\frac {4n^2 +4n + 1 -5}{4})^2 = (\frac {4n^2 +4n -4}{4})^2=$

$(n^2 +n - 1)^2$.

====

So ....

If $x$ is the first integer and $\frac {2n + 1}2 = x + \frac 32$ then

$n = x + 1$.

So $x(x+1)(x+2)(x+3) + 1 = ((x+1)^2 + (x+1) - 1)^2 = (x^2 + 3x +1)^2$

....

So as you got $x^4 + 6x^3 + 11x^2 + 6x + 1$ that actually equals $(x^2 + 3x +1)^2$

Indeed $x^4 + 6x^3 + 11x^2 + 6x + 1 = x^2(x^2 + 3x + 1) + 3x^3 +10x^2 + 6x + 1$

$= x^2(x^2 + 3x+ 1) + 3x(x^2 + 3x + 1) +x^2 +3x + 1$

$= (x^2 + 3x + 1)^2$.

.... addendum.....

D'oh.

If $x(x+1)(x+2)(x+3) + 1 = a^2$ then

$x(x+ 1)(x+ 2)(x+3) = a^2 - 1 = (a + 1)(a-1)$

To get factors that close together they'd have to be

$a = x(x+3) \pm 1= (x+ 1)(x+2) \mp 1$

and indeed $a= x(x+3) + 1 = (x+1)(x+2) - 1= x^2 +3x + 1$.

proves the statement! (If we work backwards.)

Answer 12

Suppose that you have 4 consecutive numbers $a, b, c, d$. They can be expressed as $a=t-\frac{3}{2}$, $b=t-\frac{1}{2}$, $c=t+\frac{1}{2}$ and $d=t+\frac{3}{2}$ for some number $t$.

Now, $$ad = \left(t-\frac{3}{2}\right)\left(t+\frac{3}{2}\right) = t^2 - \left(\frac{3}{2}\right)^2 = t^2 - \frac{9}{4}$$ and $$bc = \left(t-\frac{1}{2}\right)\left(t+\frac{1}{2}\right) = t^2 - \left(\frac{1}{2}\right)^2 = t^2 - \frac{1}{4}$$

If we define $y = t^2 - \frac{5}{4}$, we have $$ad = \left(t-\frac{3}{2}\right)\left(t+\frac{3}{2}\right) = y - 1$$ and $$bc = \left(t-\frac{1}{2}\right)\left(t+\frac{1}{2}\right) = y + 1$$

Furthermore, since the LHS in both cases is an integer, it is clear that $y$ is an integer.

So the product of all four numbers is $$ abcd = (y - 1)(y+1) = y^2 - 1 $$ one less than the square of an integer.

Answer 13

This is another way of looking at @jwg's answer.

Let the four consecutive numbers be $a,b,c,d$ and let $t$ be the number half-way between $b$ and $c$. Then

\begin{align} abcd + 1 &= \bigg(t-\frac 32\bigg)\bigg(t-\frac 12\bigg) \bigg(t+\frac 12\bigg)\bigg(t+\frac 32\bigg) + 1\\ &= \bigg(t^2-\frac 94\bigg)\bigg(t^2-\frac 14\bigg) + 1\\ &= t^4 - \frac 52 t + \frac{25}{16}\\ &= \bigg(t^2 - \frac 54 \bigg)^2 \end{align}

Letting $t = a + \frac 32$, we get

\begin{align} abcd + 1 &= \bigg(t^2 - \frac 54 \bigg)^2 \\ &= \bigg(a^2 +3a + \dfrac 94 - \frac 54 \bigg)^2 \\ &= (a^2 +3a + 1)^2 \end{align}

This suggests the following solution.

\begin{align} abcd + 1 &= a(a+1)(a+2)(a+3) + 1 \\ &= a(a+3) \cdot (a+1)(a+2) + 1 \\ &= (a^2+3a) (a^2+3a+2) + 1 \\ &= (a^2+3a+1 \ - \ 1)(a^2+3a+1 \ + \ 1) + 1 \\ &= (a^2+3a+1)^2 - 1 + 1 \\ &= (a^2+3a+1)^2 \end{align}