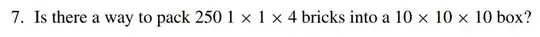My question isn't specifically about the problem below, but about coloring proofs in general. From what I've seen about coloring proof problems thus far, I've noticed that we form a conditional and find a contradiction, i.e we can't cover a checkerboard with the 2 diagonal corner pieces removed with $2$ x $1$ pieces, or find cases where we could fit certain pieces onto a board. But I'm unsure how these conditionals are formed since the proofs I've seen usually don't do so explicitly. For the problem below, would we write if we could fit $250$ $4$x$1$x$1$ bricks in a $10$x$10$x$10$ box with the coloring as such, then each brick would contain each color. Or do we write if we could fit these pieces into the box then each brick would contain 4 different colors?
Thanks
- Solution