1

Let's say we have an equation: $$\frac{x^3}{3}-a^2x+b=0$$ where $a$ and $b$ are randomly picked from an interval (0,1). Let $N$ be a number of real roots of the equation (so $N$ can be $1$ or $3$). How do I find the probability of $N$ being $1$?

I'm assuming that the probability of picking a number from (0,1) is uniformly distributed, so: $$a,b\in\mathcal{U}(0,1)$$ How do I go from there?

BruceET
  • 51,500
A6EE
  • 313
  • Do you know the criterion for when a cubic has one, two, or three real roots? (The middle option is possible if there's a double real root.) – Brian Tung Jun 25 '18 at 15:22
  • @BrianTung If the cubic has 2 real roots, then it has 3 real roots. It is not possible for two real and one complex root, so the middle option is not possible. – SlipEternal Jun 25 '18 at 15:27
  • 1
    This has been asked here before, without an answer (but with a lot more effort put into it). – joriki Jun 25 '18 at 15:46
  • Similar Q & A & Refs, but for quadratic. Why not start by showing some of your efforts? At least, state criterion for one real root of cubic? Suggest approaches? (Or are you just totally outscourcing this?) – BruceET Jun 25 '18 at 18:20
  • @InterstellarProbe: I'm talking about the situation where there's two real roots, one of multiplicity two. If that's considered three real roots, then shall we also consider the one real root of $y = x^3$ three roots as well? That's a single root of multiplicity three. – Brian Tung Jun 25 '18 at 19:47
  • @InterstellarProbe: Of course, as regards this problem, that's not a concern. These are events of measure zero on the interval of concern. I'm just pointing out that someone might consider (say) $y = x^3-x^2$ to have two real roots: one at $x = 0$ and one at $x = 1$. – Brian Tung Jun 25 '18 at 19:49

2 Answers2

3

Comment: According to Wikipedia on 'Cubic function', the equation $\alpha x^3 + \beta x^2 + \gamma x + \delta = 0$ has only one real root, if $$\Delta = 18\alpha\beta\delta\gamma - 4\beta^3\delta + \beta^2\gamma^2 - 4 \alpha\gamma^3 - 27\alpha^2\delta^2 < 0.$$

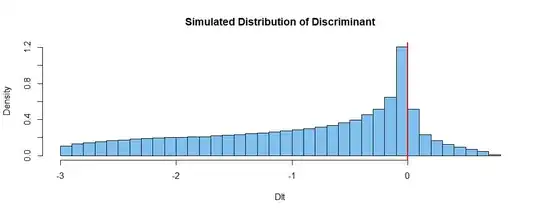
For our cubic equation $\frac 1 3x^2 - A^2x + B = 0,$ we have $\alpha = 1/3, \beta=0, \gamma=-A^2,$ and $\delta = B,$ so the discriminant becomes $\Delta = \frac 4 3 A^6 - 3B^2.$ If $A$ and $B$ are independently distributed as $\mathsf{Unif}(0,1),$ then it should not be difficult to find $P(\Delta < 0).$

Because OP has shown no engagement, I expect this Question might be closed soon. In this comment, I will show only the approximate value $P(\Delta < 0) = 0.875,$ obtained from an easy simulation in R. (A million iterations should give 3-place accuracy; three such simulations agree to three places.)

a = runif(10^6);  b = runif(10^6); Dlt = .75*a^6 - 3*b^2
mean(Dlt < 0)
## 0.875421

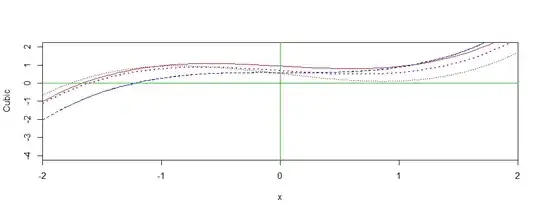
enter image description here

Here are four of the one million cubic curves in the simulation above. All of them happen to have one real root (each at $x < -1);$ one of them 'almost' had three real roots.

enter image description here

BruceET
  • 51,500
0

The cubic equation $f(x)=\frac{x^3}{3}-a^2x+b=0$ has two real roots (a single root and a double root) when it has two turning points, and one of these corresponds to a zero value of the cubic, i.e. if there is an $x$ such that $f(x)=f'(x)=0$. Since $f'(x)=x^2-a^2$ and $f'(x)=0$ when $x=\pm |a|$, that leads to the possibilities:

  • $b=\tfrac23 |a|^3$ with the double root at $x=|a|$ and single root at $x=-2|a|$
  • $b=-\tfrac23 |a|^3$ with the double root at $x=-|a|$ and single root at $x=2|a|$

In this question we are looking for one real root, which quick investigation suggests happens when $b$ is outside these two possibilities i.e. $\mathbb P( b<-\tfrac23 |a|^3) + \mathbb P( b > \tfrac23 |a|^3)$.

Here $a$ and $b$ are independently distributed uniformly on $[0,1]$ so $|a|=a$ and $\mathbb P( b< -\frac23 |a|^3)=0$. So overall the probability is $$\mathbb P\left( \frac23 a^3 < b \le 1 \right)=\int\limits_0^{1} \left(1-\frac23 a^3\right) \,da= \frac56 \approx 0.833$$

Henry
  • 157,058