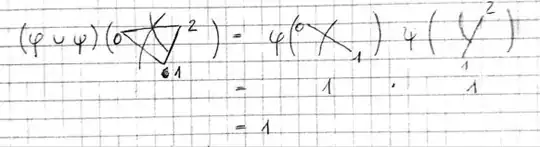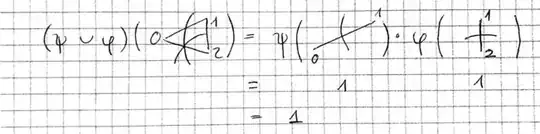7

I am trying to understand Hatcher's first example on cup product, calculating it for the orientable genus 2-surface:enter image description here

He wants to calculate $\phi_1\smile\psi_1$ for $\phi_1,\psi_1$ the cohomology classes dual to $a_1,b_1$. To choose representatives (which I may denote the same way), we have to state what $\phi_1$ and $\psi_1$ do on arbitrary 1-chains. To make them cocycles, we can chose $\phi_1$ in such a way that it assigns to an edge the number of times it crosses the arc $\alpha_1$, and similarly for $\psi_1$ (possibly with orientation…).

Now, let $\sigma$ be the triangle in the bottom right, with outer edge $b_1$. We number its corners such that 0 is the center and $b$ goes from 1 to 2. Then $(\phi_1\smile\psi_1)(\sigma)=\phi_1(\sigma|_{[01]})\psi_1(\sigma|_{[12]})=1$ since the radius $\sigma|_{[01]}$ crosses $\alpha_1$ and $b_1=\sigma|_{[12]}$ crosses $\beta_1$.

But if I take $(\psi_1\smile\phi_1)(\sigma)=\psi_1(\sigma|_{[01]})\cdot\phi_1(\sigma|_{[12]})=0$ since $b_1=\sigma|_{[12]}$ does not cross $\alpha_1$.

This is certainly wrong, but starting from which point?

Edit: Concerning @kenny-wong's answer: How can I see that $\psi\smile\phi$ evaluates to $-1$ on the right hand triangle? I would have thought that I could have calculated as follows:

enter image description here

which yields the correct $(\phi\smile\psi)(\sigma)=1$ (since all other triangles yield zero), but

enter image description here

also yields $+1$ instead of the expected $-1$. How do I correct this?

Bubaya
  • 2,204
  • 9
  • 20

1 Answers1

8

Edit: I realise that your concern is about why $\psi_1 \smile \phi_1$ is does not appear to be equal to $ - \phi_1 \smile \psi_1$. My original answer didn't address this point directly, so let me address it:

The statement $\psi_1 \smile \phi_1 = - \phi_1 \smile \psi_1$ is only true when we view $\psi_1 \smile \phi_1$ and $- \phi_1 \smile \psi_1$ as functions on the homology classes in $H_2(X, \mathbb Z)$. It does not hold at the level of individual 2-chains. (The proof in Hatcher uses a chain homotopy argument, which is only valid at the level of homology.)

In the context of this particular example, this means there is no reason why $\psi_1 \smile \psi_1(\sigma)$ should be equal to $- \psi_1 \smile \phi_1(\sigma)$ when $\sigma$ represents a single triangle in the diagram. However, if $s$ represents a generator of $H_2(X, \mathbb Z)$ (so $s$ is a sum of all eight triangles in the diagram), then the equality $\psi_1 \smile \phi_1(s) = - \phi_1 \smile \psi_1 (s)$ must hold.

Let's check this. With the vertex numbering as stated in the book (see also my original answer below, where I've spelt out the choice of numbering), $\phi_1 \smile \psi_1 (s)$ receives a contribution of $1$ from the bottom-right triangle, and no contributions from any other triangle. Meanwhile $\psi_1 \smile \phi_1(s)$ receives no contribution from the bottom-right triangle; however, it receives a contribution of $-1$ from the right-hand triangle, which means that $\psi_1 \smile \phi_1 (s) = -1$. So everything works out.

Original answer: (Addressing the issue of renumbering of vertices, which is a major source of confusion here, but turns out not to be what motivated the question.)

Singular homology/cohomology

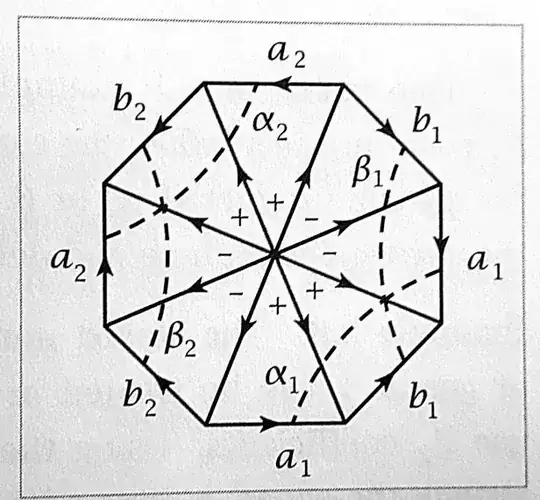
Hatcher's ultimate goal is to compute the action of $\phi_1 \smile \psi_1$ on a generator of $H_2(X,\mathbb Z)$. As a representative of the generator of $H_2(X, \mathbb Z)$, he uses the sum of the eight triangles shown in the diagram. The interesting thing is that only certain choices of vertex numbering will ensure that the singular 2-chain formed by summing the eight triangles has zero boundary.

So why is this? In singular homology, the boundary of $[0,1,2]$ is $[0,1] + [1,2] - [0,2]$, whereas the boundary of $[2,0,1]$ is $[0,1] - [2,1] + [2,0]$. These are different singular $1$-chains! In the definition of singular homology, there is no explicit provision for identifying $[2,1]$ as the same as $-[1,2]$, or for identifying $[2,0]$ as the same as $-[0,2]$. Therefore, when we number the vertices on our eight triangles, we must take care that the boundaries really do cancel out, bearing in mind that $[i,j]$ is not explicitly declared equal to $-[j,i]$ in the group of singular 1-chains.

One numbering that works is to take the "centre" vertex to be the $0$ vertex of each of the eight triangles. The triangles marked "$+$" (resp. "$-$") then have vertices $1$ and $2$ assigned in an anti-clockwise (resp. clockwise) fashion, and are weighted with coefficients of $+1$ (resp. $-1$). You can easily verify that this numbering ensures that the boundary of the sum of the eight triangles is zero. With this choice of numbering, the only triangle that contributes to the action of $\phi_1 \smile \psi_1$ is the bottom-right triangle, and this triangle contributes a value of $1$.

Simplicial homology/cohomology

What's different here is that $[i,j]$ is usually defined to be the same as $-[j,i]$ in simplicial homology. This gives you the flexibility to number your vertices however you like, without needing to worry about proper cancellations of boundaries. Unfortunately, this causes annoying ambiguities when you evaluate cup products.

This math.SE question discusses this issue. In particular, see Jim Belk's answer, in which he proposes the symmetrised definition $$ \phi_1 \smile \psi_1 ([0,1,2]) = \frac 1 {3!} \sum_{\sigma \in S_3}(-1)^\sigma \phi_1([\sigma(0), \sigma(1)]). \psi_1([\sigma(1), \sigma(2)]).$$

With this definition, you will find that the bottom-right triangle contributes only $\frac 1 2 $ to action of the cup product; however, the right-hand triangle contributes the remaining $\frac 1 2 $, ensuring that the action of the cup product on the generator of $H_2(X, \mathbb Z)$ is $1$.

Kenny Wong
  • 32,192
  • Thank you for your detailed response; the first point is something I haven't had in mind. However, I still don't get the other half. How would I see that $\phi\smile\psi(\sigma)=-\psi\smile\phi(\sigma)$ if calculated in terms of singular homology? And shouldn't there be any problem if I fix an order of vertices once and for all? However, in the latter case, why isn't $\psi\smile\phi(\sigma)=0$? – Bubaya Jun 23 '18 at 21:25
  • @Bubaya Apologies - I misunderstood your concerns. I've edited the answer. – Kenny Wong Jun 23 '18 at 21:49
  • Ah, of course, it makes perfect sense that I cannot assume this to hold when evaluated on chains, since, as you mention, one relies on homotopies for the proof. However, When I take the entire sum of all triangles, obtain a +1 from the right triangle (see my edited question), instead of the expected -1. Can you help me figuring out why? – Bubaya Jun 24 '18 at 08:39
  • @Bubaya The correct numbering of the right-hand triangle is to take the "centre" vertex to be the $0$ vertex, then have the vertices $1$ and $2$ assigned in a clockwise fashion. So the second of your two pictures is the correct one. Thus, $\psi \smile \phi$ acting on the right-hand triangle gives $+1$, as you have found. However, the generator of $H_2(X, \mathbb Z)$ is bottom + bottom-right - right - top-right + top + top-left - left - bottom-left. Because of the minus coefficient for the right triangle in this summation, we see that $\psi \smile \phi$ acting on the generator gives $-1$. – Kenny Wong Jun 24 '18 at 09:15
  • @Bubaya I have spelt out Hatcher's choice of numbering in my paragraph starting "One numbering that works...". Have you checked that this choice of numbering is a good choice, i.e. that the boundary of the sum of the eight triangles evaluates to zero, without the need to explicitly identify edges of the form $[i,j]$ with edges of the form $-[j,i]$? – Kenny Wong Jun 24 '18 at 09:17
  • Ah, I got it. Thank you. – Bubaya Jun 24 '18 at 11:44
  • My problem in understanding was, despite of the numbering varying across the triangles between clockwise and anticlockwise, that I should consider every triangle to be oriented in the same direction (such that there are triangles $[0,1,2]$ and $[0,2,1]$). Of course, if I don't do this, the interior edges won't cancel. – Bubaya Jun 24 '18 at 17:58
  • This part of Hatcher is definitely unclear. Great answer! – JZweifler Feb 01 '24 at 07:01