Trying to find the solutions of $3np+3n+2=n^2+p^2$ with n and p positive integers, I found out n=14 and p=4 is a solution, but I want to know if there are others.
3 Answers
This is a slight variant of Vieta Jumping. For a given solution $(n,p)$ we can travel around the given hyperbola by $$ (n,p) \mapsto (3p+3 - n, p) $$ and $$ (n,p) \mapsto (n, 3n-p) $$ To keep going, alternate the maps. If you double any mapping you go back where you started
It is also possible to separate the variables. The sequence of $n$ values obeys $$ n_{j+2}= 7 n_{j+1} - n_j + 6 \; , $$ while the sequence of $p$ values obeys the similar $$ p_{j+2}= 7 p_{j+1} - p_j + 9 \; . $$ Each $n$ or $p$ value occurs in two consecutive solutions, owing to the zigzag way the solutions move out on the two branches of the hyperbola in the first quadrant.
 probably better to make vertical
$$ (1,4) $$
$$ (14 , 4 )$$
$$ (14 , 38 )$$
$$ (103 , 38 )$$
$$ (103 , 271 )$$
$$ (713 , 271 )$$
$$ (713 , 1868 )$$
$$ (4894 , 1868 )$$
$$ (4894 , 12814 )$$
$$ (33551 , 12814 )$$
$$ (33551 , 87839 )$$
$$ (229969 , 87839 )$$
$$ (229969 , 602068 )$$
$$ (1576238 , 602068 )$$
$$ (1576238 , 4126646 )$$
$$ (10803703 , 4126646 )$$
$$ (10803703 , 28284463 )$$
$$ (74049689 , 28284463 )$$
$$ (74049689 , 193864604 )$$
$$ (507544126 , 193864604 )$$
$$ (507544126 , 1328767774 )$$
$$ (3478759199 , 1328767774 )$$
$$ (3478759199 , 9107509823 )$$
$$ (23843770273 , 9107509823 )$$
$$ (23843770273 , 62423800996 )$$
$$ (163427632718 , 62423800996 )$$
$$ (163427632718 , 427859097158 )$$
$$ (1120149658759 , 427859097158 )$$
$$ (1120149658759 , 2932589879119 )$$
$$ (7677619978601 , 2932589879119 )$$
$$ (7677619978601 , 20100270056684 )$$
$$ (52623190191454 , 20100270056684 )$$
$$ (52623190191454 , 137769300517678 )$$
$$ (360684711361583 , 137769300517678 )$$
$$ (360684711361583 , 944284833567071 )$$
$$ (2472169789339633 , 944284833567071 )$$
$$ (2472169789339633 , 6472224534451828 )$$
$$ (16944503814015854 , 6472224534451828 )$$
$$ (16944503814015854 , 44361286907595734 )$$
$$ (116139356908771351 , 44361286907595734 )$$
$$ (116139356908771351 , 304056783818718319 )$$
$$ (796030994547383609 , 304056783818718319 )$$
$$ (796030994547383609 , 2084036199823432508 )$$
$$ (5456077604922913918 , 2084036199823432508 )$$
$$ (5456077604922913918 , 14284196614945309246 )$$
$$ (37396512239913013823 , 14284196614945309246 )$$
$$ (37396512239913013823 , 97905340104793732223 )$$
$$ (256319508074468182849 , 97905340104793732223 )$$
$$ (256319508074468182849 , 671053184118610816324 )$$
$$ (1756840044281364266126 , 671053184118610816324 )$$
$$ (1756840044281364266126 , 4599466948725481982054 )$$
probably better to make vertical
$$ (1,4) $$
$$ (14 , 4 )$$
$$ (14 , 38 )$$
$$ (103 , 38 )$$
$$ (103 , 271 )$$
$$ (713 , 271 )$$
$$ (713 , 1868 )$$
$$ (4894 , 1868 )$$
$$ (4894 , 12814 )$$
$$ (33551 , 12814 )$$
$$ (33551 , 87839 )$$
$$ (229969 , 87839 )$$
$$ (229969 , 602068 )$$
$$ (1576238 , 602068 )$$
$$ (1576238 , 4126646 )$$
$$ (10803703 , 4126646 )$$
$$ (10803703 , 28284463 )$$
$$ (74049689 , 28284463 )$$
$$ (74049689 , 193864604 )$$
$$ (507544126 , 193864604 )$$
$$ (507544126 , 1328767774 )$$
$$ (3478759199 , 1328767774 )$$
$$ (3478759199 , 9107509823 )$$
$$ (23843770273 , 9107509823 )$$
$$ (23843770273 , 62423800996 )$$
$$ (163427632718 , 62423800996 )$$
$$ (163427632718 , 427859097158 )$$
$$ (1120149658759 , 427859097158 )$$
$$ (1120149658759 , 2932589879119 )$$
$$ (7677619978601 , 2932589879119 )$$
$$ (7677619978601 , 20100270056684 )$$
$$ (52623190191454 , 20100270056684 )$$
$$ (52623190191454 , 137769300517678 )$$
$$ (360684711361583 , 137769300517678 )$$
$$ (360684711361583 , 944284833567071 )$$
$$ (2472169789339633 , 944284833567071 )$$
$$ (2472169789339633 , 6472224534451828 )$$
$$ (16944503814015854 , 6472224534451828 )$$
$$ (16944503814015854 , 44361286907595734 )$$
$$ (116139356908771351 , 44361286907595734 )$$
$$ (116139356908771351 , 304056783818718319 )$$
$$ (796030994547383609 , 304056783818718319 )$$
$$ (796030994547383609 , 2084036199823432508 )$$
$$ (5456077604922913918 , 2084036199823432508 )$$
$$ (5456077604922913918 , 14284196614945309246 )$$
$$ (37396512239913013823 , 14284196614945309246 )$$
$$ (37396512239913013823 , 97905340104793732223 )$$
$$ (256319508074468182849 , 97905340104793732223 )$$
$$ (256319508074468182849 , 671053184118610816324 )$$
$$ (1756840044281364266126 , 671053184118610816324 )$$
$$ (1756840044281364266126 , 4599466948725481982054 )$$
mpz_class n = 1;
mpz_class p = 4;
for(int k = 1; k <= 25; ++k)
{
n = 3 * p + 3 - n;
cout << "$$ (" << n << " , " << p << " )$$ " << endl;
p = 3 * n - p;
cout << "$$ (" << n << " , " << p << " )$$ " << endl;
}
- 139,541
There are base solutions $n=-1,p=-2$ and $n=-2,p=-2$ Starting with either one, you can use either of two recurrences
$$n' = 3 n - 8 p - 12 \\ p' = 8 n - 21 p - 30$$
and also:
$$n' = - 21 n + 8 p - 12 \\ p' = - 8 n + 3 p - 6$$
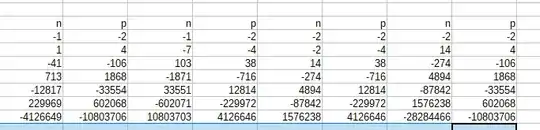
This gives the following four sets of solutions
Answers found with the help of the Alpertron, but it missed the $-2,-2$ base solution.
- 374,822
-
I don't think you have (103, 271) or (713, 271) or (33551, 87839) or ( 229969, 87839) – Will Jagy Jun 14 '18 at 00:23
This is not an answer but a request for a manual derivation of all positive integer solutions. Below is my work which hit a brick wall. If helpful, anyone is welcome to piggyback off of my work.
Re-organizing terms, $\;n^2 + n(-3p - 3) + (p^2 - 2) = 0 \;\Rightarrow\;$
$n = \frac{1}{2}\left[3p+3 \pm \sqrt{5p^2 + 18p + 17}\;\right].$
Therefore, there exists $k$ such that $3p+3+k$ is an even positive integer and
$\;5p^2 + 18p + (17-k^2) = 0 \;\Rightarrow\;$
$p = \frac{1}{10}\left[\;-18 \pm \frac{1}{2}\sqrt{5k^2 - 4}\;\right]. $
My knowledge of Pell Equations is limited to $x^2 - Dy^2 = \pm 1.$
My understanding (which could be in error) is that there has been work done on (for example) $L^2 - 5k^2 = -4.$
- 35,619
- 3
- 17
- 39
-
suggest going through the questions with https://math.stackexchange.com/questions/tagged/vieta-jumping – Will Jagy Jun 14 '18 at 03:38