An ant walk on the edges of a cube where it can select any of the 3 adjoining vertices with equal probability.

Question

There is a cube and an ant is performing a random walk on the edges where it can select any of the 3 adjoining vertices with equal probability. What is the expected number of steps it needs till it reaches the diagonally opposite vertex?

Answer 1

Extending to $d$-dimensions

So I had enough time to procrastinate today and I extended this problem to $d$ dimensions. I would appreciate if someone could read through the answer and suggest any simplification to final answer if possible. Do the final numbers $u_n$ constitute a nice well known sequence? Further, what other interesting problems arise out this ant and the cube problem. I think another nice problem is the expected cover time. Thanks

Working out explicitly for $d=3$ gave some nice hints and a good picture of what is going on. We use these to extend to any d-dimension.

The first thing is to define a cube in $d$-dimensions. A $\mathbf{d}$-dimensional cube is a set of vertices of the form $(i_1,i_2,\ldots,i_d)$ where $i_k \in \{0,1\}$. There is an edge between vertex $(i_1,i_2,\ldots,i_d)$ and vertex $(j_1,j_2,\ldots,j_d)$ if $\exists l$ such that $\left | i_l - j_l \right| = 1$ and $i_k = j_k$, $\forall k \neq l$.

Two vertices are said to be adjacent if they share an edge. It is easy to note that every vertex shares an edge with $d$ vertices. (Consider a vertex $(i_1,i_2,\ldots,i_d)$. Choose any $i_k$ and replace $i_k$ by $1-i_k$. This gives an adjacent vertex and hence there are $d$ adjacent vertices as $k$ can be any number from $1$ to $d$). Hence, the probability that an ant at a vertex will choose an edge is $\frac1{d}$.

For every vertex, $(i_1,i_2,\ldots,i_d)$ let $s((i_1,i_2,\ldots,i_d)) = \displaystyle \sum_{k=1}^d i_k$. Note that $s$ can take values from $0$ to $d$. There are $\binom{d}{r}$ vertices such that $s((i_1,i_2,\ldots,i_d)) = r$.

Let $v_{(i_1,i_2,\ldots,i_d)}$ denote the expected number of steps taken from $(i_1,i_2,\ldots,i_d)$ to reach $(1,1,\ldots,1)$

Let $S_r = \{ (i_1,i_2,\ldots,i_d) \in \{0,1\}^d: s((i_1,i_2,\ldots,i_d)) = r\}$

Claim: Consider two vertices say $a,b \in S_r$. Then $v_a = v_b$. The argument follows easily from symmetry. It can also be seen from writing down the equations and noting that the equations for $a$ and $b$ are symmetrical.

Further note that if $a \in S_r$, with $0 < r < d$, then any adjacent vertex of $a$ must be in $S_{r-1}$ or $S_{r+1}$. Any adjacent vertex of $(0,0,\ldots,0)$ belongs to $S_1$ and any adjacent vertex of $(1,1,\ldots,1)$ belongs to $S_{d-1}$. In fact, for any $a \in S_r$, $r$ adjacent vertices $\in S_{r-1}$ and $d-r$ adjacent vertices $\in S_{r+1}$.

Let $u_r$ denote the expected number of steps from any vertex $\in S_r$ to reach $(1,1,\ldots,1)$. For $r \in \{1,2,\ldots,d-1\}$, we have \begin{align} u_r & = 1 + \frac{r}{d} u_{r-1} + \frac{d-r}{d} u_{r+1} & r \in \{1,2,\ldots,d-1\}\\\ u_0 & = 1 + u_1 & r = 0\\\ u_d & = 0 & r = d \end{align} Setting up a matrix gives us a tai-diagonal system to be solved. Instead, we go about solving this as follows.

Let $p_r = \frac{r}{d}$, $\forall r \in \{1,2,\ldots,d-1\}$. Then the equations become \begin{align} u_r & = 1 + p_r u_{r-1} + (1-p_r) u_{r+1} & r \in \{1,2,\ldots,d-1\}\\\ u_0 & = 1 + (1-p_0) u_1 & r = 0\\\ u_d & = 0 & r = d \end{align} Let $a_{r} = u_{r+1} - u_r$. Then we get \begin{align} p_r a_{r-1} & = 1 + (1-p_r)a_r & r \in \{1,2,\ldots,d-1\}\\\ a_0 & = -1 & r = 0 \end{align} Note that $u_m = - \displaystyle \sum_{k=m}^{d-1} a_k$ and $u_d = 0$ \begin{align} a_0 & = -1 & r = 0\\\ a_{r} & = \frac{p_r}{1-p_r} a_{r-1} - \frac1{1-p_r} & r \in \{1,2,\ldots,d-1\} \end{align} Let $l_r = \frac{p_r}{1-p_r} = \frac{r}{d-r}$ \begin{align} a_0 & = -1 & r = 0\\\ a_{r} & = l_r a_{r-1} - (1+l_r) & r \in \{1,2,\ldots,d-1\} \end{align} \begin{align} a_1 &= l_1 a_0 - (1+l_1)\\\ a_2 & = l_2 l_1 a_0 - l_2(1+l_1) - (1+l_2)\\\ a_3 & = l_3 l_2 l_1 a_0 - l_3 l_2 (1+l_1) - l_3 (1+l_2) - (1+l_3)\\\ a_m & = \left( \prod_{k=1}^{m} l_k \right) a_0 - \displaystyle \sum_{k=1}^{m} \left((1+l_k) \left( \prod_{j=k+1}^m l_j \right) \right) \end{align} Since $a_0 = -1$ and $l_0 = 0$, we get \begin{align} a_m & = - \displaystyle \sum_{k=0}^{m} \left((1+l_k) \left( \prod_{j=k+1}^m l_j \right) \right) \end{align} Hence, \begin{align} u_n & = - \displaystyle \sum_{m=n}^{d-1} a_m\\\ u_n & = \displaystyle \sum_{m=n}^{d-1} \left( \displaystyle \sum_{k=0}^{m} \left((1+l_k) \left( \prod_{j=k+1}^m l_j \right) \right) \right)\\\ u_n & = \displaystyle \sum_{m=n}^{d-1} \left( \displaystyle \sum_{k=0}^{m} \left(\frac{d}{d-k} \left( \prod_{j=k+1}^m \frac{j}{d-j} \right) \right) \right)\\\ u_n & = \displaystyle \sum_{m=n}^{d-1} \frac{\displaystyle \sum_{k=0}^{m} \binom{d}{k}}{\binom{d-1}{m}} \end{align} Note that \begin{align} u_n & = \frac{\displaystyle \sum_{k=0}^{n} \binom{d}{k}}{\binom{d-1}{n}} + u_{n+1} & \forall n \in \{0,1,2,\ldots,d-2 \} \end{align} The expected number of steps from one vertex away is when $n = d-1$ and hence $u_{d-1} = 2^d-1$

The expected number of steps from two vertices away is when $n = d-2$ and hence $u_{d-2} = \frac{2d(2^{d-1} - 1)}{d-1}$

The answers for the expected number of steps from a vertex and two vertices away coincide with Douglas Zhare's comment

---

Initial Solution

Problems such as these fall in the category of Markov chains and one way to solve this is through first step analysis.

We shall denote the vertices of the cube by numbers from $1$ to $8$ with $1$ and $8$ being the opposite ends of the body diagonal.

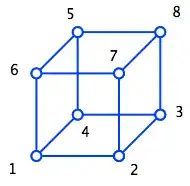
Let $v_i$ denote the expected number of steps to reach the vertex numbered $8$ starting at vertex numbered $i$.

$v_1 = 1 + \frac{1}{3}(v_2 + v_4 + v_6)$; $v_2 = 1 + \frac{1}{3}(v_1 + v_3 + v_7)$; $v_3 = 1 + \frac{1}{3}(v_2 + v_4 + v_8)$; $v_4 = 1 + \frac{1}{3}(v_1 + v_3 + v_5)$; $v_5 = 1 + \frac{1}{3}(v_4 + v_6 + v_8)$; $v_6 = 1 + \frac{1}{3}(v_1 + v_5 + v_7)$; $v_7 = 1 + \frac{1}{3}(v_6 + v_2 + v_8)$; $v_8 = 0$;

Note that by symmetry you have $v_2 = v_4 = v_6$ and $v_3 = v_5 = v_7$.

Hence, $v_1 = 1 + v_2$ and $v_2 = 1 + \frac{1}{3}(v_1 + 2v_3)$ and $v_3 = 1 + \frac{2}{3} v_2$.

Solving we get $$\begin{align} v_1 & = 10\\ v_2 = v_4 = v_6 & = 9\\ v_3 = v_5 = v_7 & = 7 \end{align}$$

Hence, the expected number of steps to reach the diagonally opposite vertex is $10$.

Answer 2

Call the set containing only the starting vertex $A$. You can move to any of three vertices next. Call the set of them $B$. For the next step, you can go back to $A$, or you can move on to any of three new vertices. Call the set of those vertices $C$. Finally, call the set containing the goal vertex $D$.

Call the expected number of steps from $A$ to $D$ $E(AD)$ etc.

Consider $E(BD)$. We can write an equation for $E(BD)$ by considering what happens if you start at $B$ and take two steps. You could go to $C$ and then to $D$. The probability of this is $2/3$ for the first step and $1/3$ for the second, or $2/9$ over all.

You could also go to $C$ and back, or to $A$ and back. Either way, your new expected number of steps to $D$ is the same as it was before, because you're back where you started. The probability of this is $7/9$ because probabilities add to one.

This gives

$E(BD) = 2/9(2) + 7/9(2 + E(BD))$

which means

$E(BD) = 9$

It takes one step to go from $A$ to $B$, so

$E(AD) = 10$

Answer 3

Hint: there are three kinds of vertices besides the target itself: 1) those one step from the target 2) those two steps from the target 3) the vertex opposite to the target Let u_i be the expected number of steps, starting at a vertex of type i, until it reaches the target. Considering the possibilities for the first step from a vertex of type i, write three equations expressing u_i in terms of the other u_j. Then solve.

Answer 4

Here is what I thought. It is a Markov Chain Problem.

Mark the start point as $E_3$, here we define $E_n$ which means that it takes $n$ sides to reach the final point. we have such relationship: take one side, it will definitely go to point as $E_2$:

$$E_3 = E_2 + 1$$

the probability is 2/3 to $E_1$ and 1/3 back to $E_3$:

$$E_2 = 2/3 (E_1 + 1) + 1/3 (E_3 + 1)$$

similar to $E_1$:

$$E_1 = 1/3 + 2/3 (1 + E_2)$$

solve these equations, you will get $E_3$ = 10.

Answer 5

The other answers are great and probably the best way to solve this problem, but here's another approach just for fun.

cube with labeled vertices for reference

The goal is to determine the expected number of steps required to move from vertex A to vertex H.

We will parameterize each vertex by the minimum number of steps $d$ away from vertex H. So for vertex A, $d=3$. Vertices B, C, and E have $d=2$. Vertices D, G, and F have $d=1$, and vertex H has $d=0$.

We will denote the probability of moving from a vertex with $d=i$ to one with $d=j$ $p_{ij}$.

By looking at the cube figure,

$p_{32}=1$ since you can't move any further from the target vertex

$p_{23}=1/3$ , $p_{21}=2/3$

$p_{12}=2/3$ , $p_{10}=1/3$

ALet $x_{ij}$ be the number of times moved from a vertex with $d = i$ to one with $d=j$.

Since we stop at the condition of reaching vertex H ($d=0$), $x_{10}=1$, as we only want to move there once. In order to have a complete path from vertex A to vertex H, $x_{21} \geq 1$, $x_{32} \geq 1$. Furthermore, the number of steps backward from a vertex must be one less than the number of forward steps. Thus $x_{23} = x_{32}-1$, $x_{12} = x_{21}-1$.

Therefore the probability of a path with $x_{32}$ transitions from $d=3$ to $d=2$ and $x_{21}$ transitions from $d=2$ to $d=1$ is just the probability of each transition raised to the number of those transitions.

$Pr(x_{32},x_{21}) = a p_{32}^{x_{32}}p_{21}^{x_{21}}p_{12}^{x_{21}-1}p_{23}^{x_{32}-1} p_{10}$

Where $a$ is the number of possible arrangements of those transitions.

Using $p_{32}=1$, $p_{10}=p_{23}$, and $p_{12}=p_{21}$, this can be rewritten as

$Pr(x_{32},x_{21}) = a p_{21}^{2x_{21}-1}p_{23}^{x_{32}}$.

Determining $a$ is somewhat tricky. The first transition and last transition are fixed. All the transitions from a vertex of $d=2$ to $d=1$ must be followed by the reverse except for the last one. Otherwise we would have reached the target vertex prematurely. Likewise all the transitions from a vertex of $d=3$ to $d=2$ must be followed by the reverse, as you can't be further away. This means transitions from $d=1$ to $d=2$ and from $d=2$ to $d=3$ can not be freely arranged. Also the last transition from $d=2$ to $d=1$ must be the second to last transition, occurring right before the transition to the target vertex. This leaves the number of transitions to be freely arranged in any order is

$x_{23}+x_{21}-1$.

The number of ways we can arrange $x_{23}$ transitions in $x_{23}+x_{21}-1$ total transitions is

${x_{23}+x_{21}-1}\choose x_{23}$ or, by writing $x_{23}$ in terms of $x_{32}$, ${x_{32}+x_{21}-2}\choose {x_{32}-1}$.

By substituting a for this we arrive at the probability we are looking for.

$ Pr(x_{32},x_{21}) = {{x_{32}+x_{21}-2}\choose{x_{32}-1}} p_{21}^{2x_{21}-1} p_{23}^{x_{32}}$.

The total number of transitions for a path with $x_{32}$ transitions from $d=3$ to $d=2$ and $x_{21}$ transitions from $d=2$ to $d=1$ is $2x_{32} + 2x_{21} -1$.

Therefore to determine the expected number of transitions, $n_{trans}$, we multiply this by the probability and sum over $x_{32}$ and $x_{21}$ from 1 to $\infty$.

$\left<n_{trans}\right> = \sum\limits_{x_{21}=1}^\infty\sum\limits_{x_{32}=1}^\infty \left(2x_{32} + 2x_{21} -1\right){{x_{32}+x_{21}-2}\choose{x_{32}-1}} p_{21}^{2x_{21}-1} p_{23}^{x_{32}} $

The result of this summation is $\left<n_{trans}\right> = 10$

Answer 6

I've been challenged whith this exercice but with a slight difference.

The difference is that if I get vertex 8 (beginning from 1) then the ant dies. And the question is "What probabilities I have to die?"

I know from the above answers that the number of expected steps from 1 to 8 is 10, then it means that is more difficult to die on vertex 8 than in vertex for example 7, due to the expected number of steps to reach vertex 7 is smaller than in vertex 8 and that means that the probability to die is higher on vertex 7 because of is easier to reach. But...I don't know exactly how to express it in terms of PROBABILITY.

Anyone could open my mind? Thanks