0

Assume that we have been asked to find the value of $\sin (18^\circ)$. We know that there are many ways to find it out. However, I'll be going with golden ratio! Let's draw a triangle whose apical angle is $36^{\circ}$. Note that this is an isosceles triangle, otherwise we couldn't apply it.

enter image description here

Consider $|BC| = 2$, from property of height, we have that $|BD| = 1$ and $|DC| = 1$. Hence I got a right triangle whose one angle is $18^{\circ}$. Now I almost found it.

$$\sin (18^{\circ}) = \dfrac{1}{2\varphi} = \dfrac{1}{\sqrt 5 + 1} = \dfrac{\sqrt 5 - 1}{4} $$

where $\varphi = \dfrac{1+\sqrt 5}{2}$.

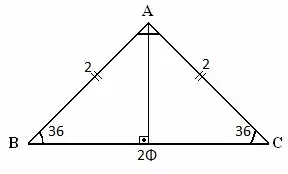
Now consider we have been asked to find the value of $\cos (36^{\circ})$. Here I have to draw a triangle whose base angles are $36^{\circ}$.

enter image description here

From the triangle, we have that

$$\cos 36^{\circ} = \dfrac{\varphi}{2} = \dfrac{1+ \sqrt 5}{4}$$

Then what about $\sin (28^{\circ})$? I mean can we apply it for other trigonometric values?

Regards!

ACB
  • 3,713
Busi
  • 572
  • 1
    How did you determine $\phi$ ? – Nehal Samee Jun 08 '18 at 11:03
  • @NehalSamee I'm editing it now. – Busi Jun 08 '18 at 11:03
  • @projectilemotion My apologies, I had thought that it doesn't work. – Busi Jun 08 '18 at 11:05
  • It happens that $\cos\pi/5$ is half the golden ratio (but you have to prove that, here you didn't prove anything), and thus the golden ratio can be linked with some angles of the form $k\pi/(5\cdot2^p)$. (that's why the golden ratio appears in many places in a pentagon). However, you can't apply this to other angles in general. And most angles of the form $\pi/n$ do not lead to trigonometric functions with nice expressions with radicals. So basically, this is an exceptional situation. – Jean-Claude Arbaut Jun 08 '18 at 11:16
  • @Jean-ClaudeArbaut In pentagon, all the triangles you can see are favorable to apply golden ratio theorem. As stated in my perspective, there should be a way to find other trigonometric values. – Busi Jun 08 '18 at 11:17
  • You can find some trigonometric values, those that lead to constructible angles. The link I give above has an answer that explains a bit and points to the Gauss-Wantzel theorem. You can compute trig functions for angles $\pi/5$ and $\pi/17$, but not $\pi/7$, $\pi/11$ nor $\pi/13$. The constructible angles are the exception. But indeed, Gauss found a construction of the $17$-gon. However, appart from those which are closely linked with $\pi/5$, you will not find the golden ratio there. – Jean-Claude Arbaut Jun 08 '18 at 11:36
  • @Jean-ClaudeArbaut What are the trigonometric values that lead to contructible angles? and do you recommend any other way or something? – Busi Jun 08 '18 at 11:50
  • See https://en.wikipedia.org/wiki/Constructible_polygon and http://mathworld.wolfram.com/ConstructiblePolygon.html For another way, you can have a look at https://en.wikipedia.org/wiki/Cyclotomic_polynomial – Jean-Claude Arbaut Jun 08 '18 at 11:53
  • Does anyone have anohter idea concerning how to find it using golden ratio? – Busi Jun 08 '18 at 12:22
  • By 28, did you mean 18? Note that $\sin^2 18^\circ =\frac{1-\cos 36^\circ}{2}=\frac{6-2\sqrt{5}}{16}=(\frac{\sqrt{5}-1}{4})^2$. – J.G. Jun 08 '18 at 12:37
  • @J.G. Not really. I just want to find it out with the way I showed as seen. – Busi Jun 08 '18 at 12:44
  • @Busi I could understand you trying to compute $\sin 18^\circ$, or even $\sin 27^\circ$, but $\sin 28^\circ$? That's tougher. – J.G. Jun 08 '18 at 12:47
  • FYI: This answer expresses the sines and cosines of $k\cdot 3^\circ$ using the golden ratio. – Blue Jun 08 '18 at 12:50
  • @Busi you are not proving anything - so need to accept your claims...?:) I agree to the stated values. Are you allowed to use trigonometry to derive one from another? – Moti Jun 10 '18 at 00:10

0 Answers0