In one of the research paper I read that $$\mathbb{a}^T(\mathbb{b}\odot \mathbb{c})=\mathbb{b}^T \text{diag}(\mathbb{a})\mathbb{c}$$ where $\mathbb{a},
\mathbb{b},\mathbb{c}$ are vectors of same size. What is the name of above property and what does $\mathbb{b}\odot \mathbb{c}$ means? Thanks in advance. Here is the snap shot of the paper I am reading 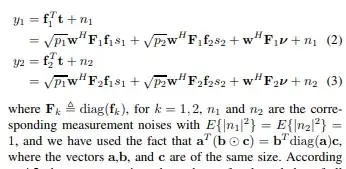
Asked
Active
Viewed 163 times
1
Blue
- 75,673
Frank Moses
- 2,718
-
2Care to share the link to the research paper you are reading? – Jose Arnaldo Bebita Dris Jun 05 '18 at 02:50
-
@JoseArnaldoBebitaDris https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6317113 page 4028, 3rd line after equation (3) – Frank Moses Jun 05 '18 at 02:53
-
1And if it’s behind a paywall just attach a screenshot of the context. – rschwieb Jun 05 '18 at 02:56
-
1Yes, I agree with @rschwieb. The article as it is is behind a paywall. – Jose Arnaldo Bebita Dris Jun 05 '18 at 02:57
-
@rschwieb I have added the screen shot of the paper. I have looked at the paper several times but I could not find where they defined the notation. – Frank Moses Jun 05 '18 at 03:03
-
1@FrankMoses it’s available for free at researchgate, for those of us who made accounts. – rschwieb Jun 05 '18 at 03:05
-
@rschwieb and I am so silly that I can not understand how your last comment answers my question in the post. – Frank Moses Jun 05 '18 at 03:08
-
1@FrankMoses I believe you now. Looks like it could be domain specific. I don’t think I’ve ever seen it. – rschwieb Jun 05 '18 at 03:09
-
1@FrankMoses it doesn’t answer your question. It points out that there is a version which is available for free. So that people can use it to help you. – rschwieb Jun 05 '18 at 03:11
-
@rschwieb oh I understand it now. I was so silly that I thought people would not have such clairvoyant insights about my sillyness and will avoid making such statements about my sillyness. – Frank Moses Jun 05 '18 at 03:16
-
Turns out to be related: https://math.stackexchange.com/a/52581/29335 – rschwieb Jun 05 '18 at 10:35
1 Answers
1
The notation ${\rm diag}({\bf a})$ is defined in the paper you linked, page 4027, column 1, last line. I have never used the notation $\odot$ but suspect that it is the elementwise product of two vectors, in which case for ${\bf a}=(a_1,a_2,\ldots,a_n)$ etc we have $$\eqalign{ {\bf a}^T({\bf b}\odot{\bf c}) &=\pmatrix{a_1&\cdots&a_n\cr}\pmatrix{b_1c_1\cr\vdots\cr b_nc_n\cr}\cr &=a_1b_1c_1+\cdots+a_nb_nc_n\cr &=\pmatrix{b_1&\cdots&b_n\cr}\pmatrix{a_1c_1\cr\vdots\cr a_nc_n\cr}\cr &=\pmatrix{b_1&\cdots&b_n\cr}\pmatrix{a_1&\cdots&0\cr\vdots&\ddots&\vdots\cr0&\cdots&a_n\cr}\pmatrix{c_1\cr\vdots\cr c_n\cr}\cr &={\bf b}^T{\rm diag}({\bf a}){\bf c}\ .\cr}$$
David
- 82,662
-
Thank you so much for your answer. I also think this is the case but they should have mentioned it in the paper – Frank Moses Jun 05 '18 at 03:19
-
Good detective work. I've seen a couple things denoting the Hadamard/Schur/elementwise product, but not this. Actually, it did turn up on stack exchange in a solution once before – rschwieb Jun 05 '18 at 10:34