checking which of the propositions are logically true

Question

i'm not sure i got this one right: i am supposed to check which of the propositions are logically true and to show why, and if not true then show a counter example.

the propositions:

1)$\vdash \forall x(P(x) \to Q(x)) \to (\exists x P(x) \to \exists x Q(x))$

2)$\vdash \forall x(P(x) \to Q(x)) \to (\forall x P(x) \to \forall x Q(x))$

3)$\vdash \forall x(P(x) \to P(c))$

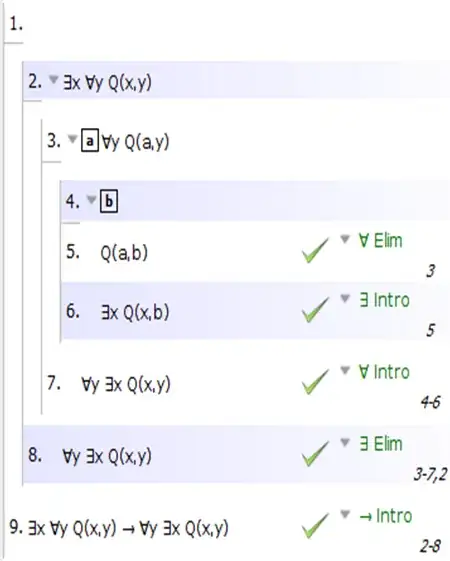
4)$\vdash \exists x \forall y Q(x,y) \to \forall y \exists x Q(x,y)$

5)$\vdash \forall y \forall x Q(x,y) \to \forall x \forall y Q(x,y)$

what i did:

1)true i think. we'll mark $P(x) \to P(d)$, $Q(x) \to Q(d)$. using twice the deduction theorem on the last part, we'll get that $(\exists x P(x) \to \exists x Q(x))$ becomes $(\exists x (P(x) \to Q(x))$.it seems logical that if it works for all x, then it should work for any x, but i don't know exactly how to fill the missing part here.

2)not true. for instance, under the domain of real numbers, if i said that p(x) equals pi and q(x) equals is rational, then $∀x(P(x)→Q(x))$ means every number that equals pi is rational, whereas $(∀xP(x)→∀xQ(x))$ means that if every real number equals pi then every real number is rational. so one is true and the other is not.

3)incorrect, but i don't know how to select an appropriate example. it seems very logical to infer that not for every x, if p(x) is true then it will still hold for p(c).

4)true.if we define a structure A so that a function B is defined as $B(x)={y \in A| A \vDash Q(x,y)}$ we can see that $∃x∀yQ(x,y)$ implies $∀y∃xQ(x,y)$ because if we look at the intersection of all B(A) being not empty, it can be inferred that B(A) itself cannot be empty, i.e, the first implies the other.

5)false. it looks quite obvious to be true, but when i look at it further it seems it is more like 3) ($\forall x(P(x) \to P(c)$),but it 2 variables, to create Q(x,y).

tried to do my best and elaborate as much as i could. if i did something wrong, please correct me so i'll be able to see the correct way and improve.

thank you very much!

Answer 1

1) is indeed true, but your reasoning is a bit confusing. How about just looking at what the statement says: If all $P$'s are $Q$'s, then if there is a $P$, then there is a $Q$. Why yes! If there is something that is a $P$, then since all $P$'s are $Q$'s, that something is also a $Q$. Hence, there is something that is a $Q$.

2) is also true: If everything is a $P$, then given that all $P$'s are $Q$'s, everything must also be a $Q$.

3) is indeed false. Just find an example, where something is a $P$, and where $c$ is not a $P$. E.g. $c$ = pi, $P$ is rational. Since $2$ is rational, $P(2)$ is true, but $P(c)$ is false, and hence $P(2) \rightarrow P(c)$ is false, and hence you don;t have that $\forall x (P(x) \rightarrow P(c))$

4) is indeed true. Your reasoning is also correct ... though a bit complicated I find. Why not: If there is something (and let's call that something 'Bob') that stands in relation $Q$ to everything, then if I pick anything, can I find something that stands in relation $Q$ to it? Of course ! Bob!

5) is true! If everything stands in relation $Q$ to everything, then everything stands in relation $Q$ to everything

Here are formal proofs for 4) and 5) created in Fitch, a Fitch-style proof system: