What are Hyperbolic Trig Functions Functions of?

Question

Circular trig functions take in an angle and spit out a ratio. What do hyperbolic functions take in (I know it's a number, but what geometrically does it represent)?

I've seen images that suggest they're a function of area, and others describe $(\cosh(t),\sinh(t))$ as a parametric, which makes me think that t is arc length covered as you move along the unit hyperbola, just like how with a circular parametric trig function t can be interpreted as arc length. It seems like it should be the function of an angle, but it isn't.

In relativity, the parameter $\zeta$ in the matrix $\begin{bmatrix} \cosh \zeta & \sinh\zeta \ \sinh\zeta & \cosh \zeta\end{bmatrix}$ is called rapidity. See Wikipedia (notice that my $\zeta$ is that page's $w$). HTH — Giuseppe Negro, May 31 '18 at 14:15
It doesn't seem to be the arc length, but it is the area between the hyperbola, the ray from the origin to the point, and the $x$-axis. Which is also true for the usual trigonometric functions on the circle. See Wikipedia's discussion of hyperbolic angles and circular angles for more. — , May 31 '18 at 14:35
From physics: the shape of https://en.wikipedia.org/wiki/Catenary is described by $\cosh (\bullet)$. — Oleg567, May 31 '18 at 14:41
@Rahul I was about to post that as an answer, but since you commented it first I will leave it for you — gen-ℤ ready to perish, May 31 '18 at 15:12
I wonder what you really want to know. Why do you expect the input to $\sinh$ and $\cosh$ to have special meaning? I assume because they are named similarily to $\sin$ and $\cos$ which seem to have special meaning for their input. But the names are more for historical reasons and that they emerge from similar considerations. $\sin$ and $\cos$ more or less coincidentally work well with angles. One can try to define "hyperbolic angles" or find geometric interpretations for the inputs to $\sinh$/$\cosh$, but it is more artificial and more driven by the similar names than necessity/geometry. — M. Winter, May 31 '18 at 15:17
Related (duplicate?): "Alternative definition of hyperbolic cosine without relying on exponential function" and "Geometric construction of hyperbolic trigonometric functions". — Blue, May 31 '18 at 16:36
@GiuseppeNegro Is that matrix supposed to have some negative signs in there? — gen-ℤ ready to perish, May 31 '18 at 21:41
@ChaseRyanTaylor: On the Wikipedia page they write $\begin{bmatrix} \cosh w & -\sinh w \ -\sinh w & \cosh w\end{bmatrix}$. If you put $w=-\zeta$ you find the matrix of my previous comment. — Giuseppe Negro, Jun 01 '18 at 08:03

gen-ℤ ready to perish · Answer 1 · 2018-05-31T16:34:47.283

The connecting factor amongst the hyperbolic and circular functions and the unit circle and hyperbola is not the angle subtended by the curve but rather the area bounded by it. Here are two images I pulled from the internet:

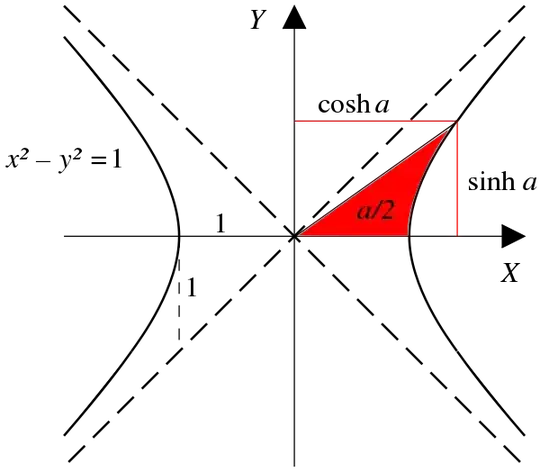
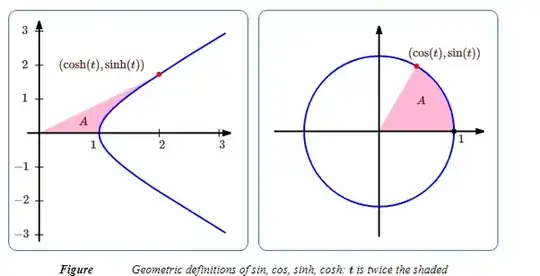
Consider the point $\mathrm H(\cosh w, \sinh w)$ on the unit hyperbola and the point $\mathrm C(\cos z, \sin z)$ on the unit circle, both plotted on the $xy$-plane. Then

$w$ equals twice the area bounded by $\rm OH$, the hyperbola, and the $x$-axis,

and since the area of the unit circle is $\pi(1)^2=\pi$, then

$z$ equals twice the area bounded by $\rm OC$, the circle, and the $x$-axis.

So to summarize, the relationship amongst the argument $t$ of any of the aforementioned functions and the area $a$ bounded by their characteristic locus is $t=2a$.

You mention “arc length covered as you move along the unit hyperbola.” Let’s consider the integral formula for arc length

$$L = \int_\alpha^\beta\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt$$

and compare the arc length $L(\mathrm H(T))$ traced along the unit hyperbola from point $(1,0)$ to $(\cosh T, \sinh T)$ and the arc length $L(\mathrm C(T))$ traced along the unit circle from point $(1,0)$ to $(\cos T, \sin T)$:

$$\begin{align} \mathrm H &: \begin{cases} x=\cosh t \\ y=\sinh t\end{cases} \\[2ex] &: \begin{cases} {dx}/{dt} = \sinh t \\ {dy}/{dt} = \cosh t\end{cases} \\[4ex] \mathrm C &: \begin{cases} x=\cos t \\ y=\sin t\end{cases} \\[2ex] &: \begin{cases} {dx}/{dt} = -\sin t \\ {dy}/{dt} = \cos t\end{cases} \end{align}$$

So

$$L(\mathrm H(T)) = \int_0^T \sqrt{ \cosh^2 t + \sinh^2 t } \, dt$$ $$L(\mathrm C(T)) = \int_0^T \sqrt{ \cos^2 t + \sin^2 t } \, dt$$

Now invoke the identities $\sin^2t+\cos^2t = 1$ but $\sinh^2t+\cosh^2t = \exp2t-\sinh(t)\cosh(t)$ and you will see that

$$L(\mathrm C(T)) = \int_0^T \sqrt{ 1 } \, dt = t\bigr|_0^T = T$$

$$\begin{align} L(\mathrm H(T)) &= \int_0^T \sqrt{ e^{2x} - {e^x-e^{-x}\over2} \cdot {e^x+e^{-x}\over2} } \, dt \\[2ex] &= \int_0^T \sqrt{ e^{2x} - {e^{2x}-1-1-e^{-2x}\over4} } \, dt \\[2ex] &= \int_0^T \sqrt{ {4e^{2x} - e^{2x}+2+e^{-2x}\over4} } \, dt \quad \cdots \end{align}$$

Does that help you see why the nice relationship seen between $t$ and $L(\mathrm C(T))$ does not emerge with $t$ and $L(\mathrm H(T))$?

What are Hyperbolic Trig Functions Functions of?

1 Answers1