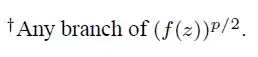1

In An Introduction to Harmonic Analysis by Katznelson I once stumbled upon this: enter image description here

with the footnote

enter image description here

Here $D$ is the complex unit disk around $0$. $f$ is holomorphic with no zeros, and since $D$ is simply connected, we have that some branch $\log(f)$ is holomorphic as proved here. So now we can define $g(z)=(f(z))^\frac{p}{2}:=\exp(\frac{p}{2}\log(f(z)))$.

Now Katznelson claims that we can take any branch. I used to ignore this part, but the more I think about it, the more I get suspicious. What if the range of $f$ has a point in the branch cut? Then this should not work.

Am I wrong, or does he mean some branch?

The Phenotype
  • 5,199

1 Answers1

2

If $f$ has no zero in the unit disk, then ANY branch of $\log f$ and of $f^\alpha$ is analytic. This follows from Monodromy Theorem (look in any course of Complex analysis). You actually cite this theorem when you write "simply connected".

(Branches of log differ only by an additive constant, if one is holomorphic then all are holomorphic). There is no such thing as a "branch cut":-) It is just an artificial tool, not something associated with a function. If you look at the proof of the monodromy theorem you see that there is no "branch cut" involved.

Alexandre Eremenko
  • 3,468
  • 19
  • 35
  • Interesting theorem. I read the wikipedia page after reading your answer and I believe I get the idea, but not the details. I believe I mixed branch and branch cut up (one is always chosen, the other not always). – The Phenotype May 31 '18 at 23:16
  • So to restate my chaotic comment as a question: $D$ is simply connected, but how do we know that $f(D)$ is simply connected, since we need this to make sure that $f(D)$ is not some domain that encircles $0$ (so $\log$ won't even be continuous)? – The Phenotype Jun 02 '18 at 12:27
  • You do not need this. If $D$ is simply connected, and $f(z)\neq 0$ in $D$, then branches of $\log f$ exist in $D$. Read Monodromy Theorem in your textbook. – Alexandre Eremenko Jun 02 '18 at 13:42
  • We can find a small disk in $D$ such that $\log f$ is analytic. My problem lies within the assumption that we can analytically continue $\log f$ along every path within $D$. Is this a well-known fact? And how can we be sure that the phenomenon from my previous comment doesn't happen (the range of $f$ containing a circle around $0$ and thus preventing any continuous/holomorphic single-valued $\log$). – The Phenotype Jun 02 '18 at 14:39
  • Analytic continuation on every path $\gamma$ is performed by the formula $\int_\gamma (f'(z)/f(z))dz.$ – Alexandre Eremenko Jun 02 '18 at 14:53
  • I get it now. Thank you so much. – The Phenotype Jun 02 '18 at 15:01