4

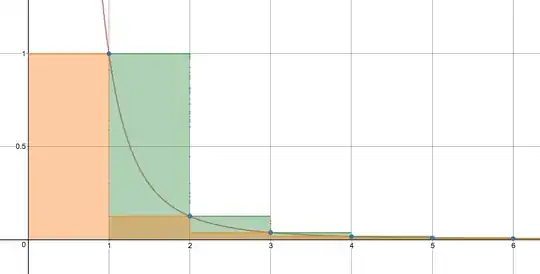
I'm trying to prove that $\frac{9}{8} < \sum\limits_{n=1}^{\infty} \frac{1}{n^3} < \frac{5}{4}$. I've seen similar proofs to this that tend to approach the proofs geometrically, using the upper and lower bounds of the remainder, the sum of the series less its $k$th partial sum, generated from the integral test. It usually involves some trick like "excluding $k$ terms." My professor tends to start at the second term to find a "lower bound," from which the proof follows with algebraic manipulation, but seemed to suggest to me that this followed from trial and error.

So, with that said, I really can't say that I understand the intuition behind finding or proving this. The first step seems to be plotting $y = \frac{1}{x^3}$ and then considering upper and lower Riemann sums (geometrically, "boxes" above the curve that will generate a sum greater than the area below it and boxes below the curve that will generate a sum less than the area below it). Though I believe I can draw the graph, I'm struggling with how to approach the problem, even if I have the abstract idea right, which I quite doubt.

I'd very much appreciate if someone could shed some light on this. Thanks in advance.

  • 3
    For a start, $1/1^3+1/2^3= 1+1/8 = 9/8$, and all the other terms are positive... – Clement C. May 28 '18 at 04:00
  • https://math.stackexchange.com/questions/2333476/series-for-zeta3-frac65 – Riemann May 28 '18 at 04:21
  • 1
    I'm not familiar with the notation from that answer, Riemann. From what I can make of it, it seems somewhat different from this question, especially with the style of proof I'm expected to use here. –  May 28 '18 at 04:23

5 Answers5

4

Approach Avoiding Integrals

Note that $$ \begin{align} \frac1{\left(n-\frac12\right)^2}-\frac1{\left(n+\frac12\right)^2} &=\frac{2n}{\left(n^2-\frac14\right)^2}\\ &\gt\frac2{n^3} \end{align} $$ Therefore, $$ \begin{align} \sum_{n=1}^\infty\frac1{n^3} &\lt1+\frac12\sum_{n=2}^\infty\left[\frac1{\left(n-\frac12\right)^2}-\frac1{\left(n+\frac12\right)^2}\right]\\ &=\frac{11}9 \end{align} $$ The other direction is simply $$ \begin{align} \sum_{n=1}^\infty\frac1{n^3} &\gt\sum_{n=1}^2\frac1{n^3}\\ &=\frac98 \end{align} $$ Thus, we get the tighter bounds $$ \frac98\lt\sum_{n=1}^\infty\frac1{n^3}\lt\frac{11}9 $$

Bounding by Integrals

Note that $$ \int_n^{n+1}\frac1{x^3}\,\mathrm{d}x\le\frac1{n^3}\le\int_{n-1}^n\frac1{x^3}\,\mathrm{d}x $$ Therefore, $$ 1+\overbrace{\int_2^\infty\frac1{x^3}\,\mathrm{d}x}^{\le\sum\limits_{k=2}^\infty\frac1{n^3}}\le\sum_{n=1}^\infty\frac1{n^3}\le1+\frac18+\overbrace{\int_2^\infty\frac1{x^3}\,\mathrm{d}x}^{\ge\sum\limits_{k=3}^\infty\frac1{n^3}} $$ Thus, $$ \frac98\le\sum_{n=1}^\infty\frac1{n^3}\le\frac54 $$

robjohn
  • 345,667
  • Is there an intuitive deduction that $\sum_{n=2}^\infty\left[\frac1{\left(n-\frac12\right)^2}-\frac1{\left(n+\frac12\right)^2}\right]<=\frac{4}{9}$ ? – Abr001am Jun 02 '18 at 15:00
  • Oh it is a telescoping series, nvm that's neat btw. – Abr001am Jun 02 '18 at 15:01
2

enter image description here See green bars for LH inequality and orange bars for RH inequality. $$\begin{align} 1+\int_2^\infty\frac 1{x^3}\; dx \quad &<\quad \sum_{n=1}^\infty \frac 1{n^3} &&<\quad 1+\frac 18+\int_2^\infty \frac 1{x^3} \; dx\\ \frac 98 \quad &<\quad \sum_{n=1}^\infty \frac 1{n^3} &&<\quad\frac 54 & \end{align}$$

Hypergeometricx
  • 22,657
1

$$\sum_{n=1}^{\infty} \frac{1}{n^3} =\sum_{n=1}^k \frac{1}{n^3} + \sum_{n=k+1}^{\infty} \frac{1}{n^3}< \sum_{n=1}^k \frac{1}{n^3}+\int_{k}^{\infty} \frac{1}{x^3} dx =\sum_{n=1}^k \frac{1}{n^3}+\frac{1}{2 k^2}$$ and this for any $k\ge 1$. For $k=2$ we get RHS $=1+1/8+1/8=5/4$.

orangeskid
  • 53,909
  • Thank you for this. Would you mind explaining where the $<$ inequality comes from? It seems to me that $\sum\limits_{n=k+1}^{\infty} \frac{1}{n^3}$ could equally represent an upper or a lower sum. I assume the comparison of this to the integral itself is what generates the inequality. Also, is the choice of $k = 2$ standard, or does it just happen to work in this particular problem? It seems that this is rather common. –  May 28 '18 at 04:39
  • We could also write $\sum_{k+1}^{\infty} >\int_{k+1}^{\infty}$, both estimates because $x\mapsto 1/x^3$ is decreasing. $k=2$ happens to work in this case. For any number larger than the sum of the series, some $k$ will work, since the difference between the remainder series and the integral approaches $0$ as $k\to \infty$, One needs some other methods if wants a better estimate, since summing up $k$ terms becomes difficult if $k$ is large. – orangeskid May 28 '18 at 04:46
  • 1
    @Matt.P If $x\in[k,k+1]$ then $0<x\le k+1$, hence $\frac1x\ge\frac1{k+1}$. My guess is that the choice $k=2$ was dictated by your question involving $\frac54$. – Mirko May 28 '18 at 04:48
0

Your intuition to attack this problem with a geometrical approach and recognizing the usefulness of the integral test in similar problems is good. Once you suspect that the integral test is going to be useful, a great way to confirm this is to draw out a few boxes of height $\frac{1}{n^3}$ starting at $1$ and ask yourself if there are easy to integrate monotonically decreasing functions that bound these boxes below or above.

Once you do this, it's clear that $\int_{k}^\infty \frac{1}{x^3} dx$ bounds the sum $\sum_{n = k}^\infty \frac{1}{n^3}$ below and the sum $\sum_{n= k + 1}^\infty \frac{1}{n^3}$ above. The rest of the problem is working out how many terms in the sum you need to take to make this bound tight enough to satisfy the prompt.

Alex Nolte
  • 4,986
  • 1
  • 12
  • 26
  • Would you mind explaining how we know that $\sum\limits_{n=k+1} \frac{1}{n^3}$ bounds the integral from above? I don't seem to be following from the geometric interpretation, which my professor described as "upper versus lower boxes," though this surely is the key to the intuition behind the proof. –  May 28 '18 at 05:02
  • Move the graph of $\frac{1}{x^3}$ right by $1$ over the plots of $\frac{1}{n^3}$ boxes. – Alex Nolte May 28 '18 at 05:04
  • I think I'm still struggling with the logic, my apologies. It seems to me that $n = k + 1$ to $\infty$ is a proper subset of the terms we'd be summing from $n = k$ to $\infty$, so by this logic it would be less than the original sum. This can't be right, surely, but I don't quite understand why. –  May 28 '18 at 05:10
  • It is! What I was saying was that $\int_{k}^\infty \frac{1}{x^3} dx$ bounds $\sum_{n=k+1}^\infty \frac{1}{n^3}$ above. By adding in the previous $k$ terms as they were, this lets us establish a nice upper bound on the sum. – Alex Nolte May 28 '18 at 05:14
  • Just to be sure I understand: that $\int_k^{\infty} \frac{1}{x^3}$ bounds the sum, $\sum_{n=k}^{\infty}$ below means that $\int_k^{\infty} \frac{1}{x^3} \leq \sum_{n=k}^{\infty}$; that this integral bounds $\sum\limits_{n=k+1}^{\infty} \frac{1}{n^3}$ above means that $\int_{n=k+1}^{\infty} \frac{1}{x^3} \ dx \leq \int_k^{\infty} \frac{1}{x^3} \ dx$; and thus $\int_{n=k+1}^{\infty} \frac{1}{x^3} \ dx \leq \int_k^{\infty} \frac{1}{x^3} \ dx \leq \sum\limits_k^{\infty} \frac{1}{n^3}$? –  May 28 '18 at 05:34
  • You're correct in what I meant by the lower bound. For the upper bound, the point is that $\sum_{n=k+1}^\infty \frac{1}{n^3} < \int_{k}^\infty \frac{1}{x^3} dx$, though that might just be a typo. This is also strictly less than $\sum_{n=k}^\infty \frac{1}{n^3}$, but that's not why we've taken this step. The point is that it gives us a straightforward way to find a number that's larger than $\sum_{i=1}^\infty \frac{1}{n^3}$. – Alex Nolte May 28 '18 at 05:57
  • 1
    Excellent. This makes more sense, thank you. –  May 28 '18 at 06:00
0

Here's another approach: \begin{align}\frac{9}{8} =\frac{1}{1^3} + \frac{1}{2^3} <\sum_{n=1}^\infty\frac{1}{n^3} = 1+\sum_{n=2}^\infty \frac{1}{n^3}<1+\sum_{n=2}^\infty\frac{1}{n^3-n} &= 1+\sum_{n=2}^\infty\frac{1}{n(n-1)(n+1)} \\ &= 1+\frac{1}{2}\sum_{n=2}^\infty\left(\frac{1}{n(n-1)}-\frac{1}{n(n+1)}\right) \\ &= 1 + \frac{1}{2}\lim_{k\to\infty}\left(\frac{1}{2}-\frac{1}{k(k+1)}\right) \\ &= \frac{5}{4}.\end{align}

Alan
  • 2,025