Area of Triangle inside a Circle in terms of angle and radius

Question

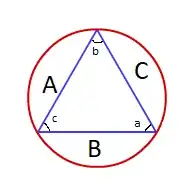
A circle $O$ is circumscribed around a triangle $ABC$, and its radius is $r$. The angles of the triangle are $\angle CAB = a, \angle ABC = b$ and $\angle ACB = c$.

The area $\triangle ABC$ is expressed by $a, b, c$ and $r$ as:

$\Large r^2 \over\Large2$$\Bigg(\sin(x)+\sin(y)+\sin(z)\Bigg)$

find $x, y$ and $z$:

My approach:

Firstly, to make it clear, I set $\overline {AB} = A$, $\overline {BC} = B$ and $\overline {CA} = C$.

$\triangle ABC= \Large{Bh \over 2}$

where $h$ is the height

$\triangle ABC = \Large{BA\sin(c) \over2}$

then, using the law of sine:

$r= \Large{A\over 2 \sin(a)} = \Large{B\over 2 \sin(b)}$

$A = 2r\sin(a)$

$B = 2r\sin(b)$

replacing on the formula of area:

$\triangle ABC = 2r^2\sin(a)\sin(b)\sin(c)$

But that doesn't help to answer the question. Is my approach correct, or else, what am I missing?

How does: "Firstly, to make it clear, I set $\overline {AB} = A$, $\overline {BC} = B$ and $\overline {CA} = C$." make it clear? — Weather Vane, May 27 '18 at 19:13
@LoveInvariants the question is unclear. It also appears to show an equilateral triangle. — Weather Vane, May 27 '18 at 19:19
And angle CAB where is that? this question needs a lot of proof reading and correcting. — ctrl-alt-delor, May 27 '18 at 19:20
I suppose the question is "Find some nice $x,y,z$ for which the area is as stated". And the hint is, consider the center of the circle and express the area of $ABC$ as the sum of areas of three triangles. — Michal Adamaszek, May 27 '18 at 19:22
Also how can we be confirmed that x,y,z are angles of a triangle — Love Invariants, May 27 '18 at 19:23
Comment on notation: usually, in this kind of problem, the angles are noted $A,B,C$, and the sides are $a,b,c$, with side $a$ opposite to the angle $A$ (same for the other two). Also, the radius of the circumcircle is noted $R$, not $r$ (which is used for the radius of the incircle). — Jean-Claude Arbaut, May 28 '18 at 04:41

Michal Adamaszek · Answer 1 · 2018-05-28T04:27:20.657

1

Let $X$ denote the center of the circle. The angles $AXB$, $BXC$ and $CXA$ are $2a$, $2b$, $2c$. Hence

$$|ABC|=|AXB|+|BXC|+|CXA|=\frac{r^2}{2}(\sin(2a)+\sin(2b)+\sin(2c))$$

where $|T|$ is the area of triangle $T$. The proof works also when the triangle is obtuse - use oriented areas.

edited May 28 '18 at 04:27

answered May 27 '18 at 19:34

Michal Adamaszek

4,018

For obtuse triangles we are required to render an angle measure greater than 180°, which does not go well with usual geometric definitions. In the long run rendering obtuse triangles as a separate case (with the offending angle measured in reverse and that triangle area explicitly subtracted) offers a "cleaner" proof. – Oscar Lanzi May 27 '18 at 23:24

Oscar Lanzi · Accepted Answer · 2018-05-27T21:50:24.220

The area formula you derived is a good one to know, but if you want something in terms of a sum of sines, use the trigonometric sum-product relations. Along the way you will also note that the angles of the rriangle sum to 180°. And be careful with signs or this won't come out pretty.

Our starting point, taking $S$ as the area:

$S=2r^2 \sin a \sin b \sin c$

Plug in $\sin a \sin b =(1/2)(\cos (a-b) - \cos (a+b))$ (watch signs!):

$S=r^2 (\cos (a-b) - \cos (a+b)) \sin c$

$S=r^2(\cos (a-b) \sin c - \cos (a+b) \sin c)$

On each of these terms use $\cos u \sin v =(1/2)(\sin (u+v) - \sin (u-v))$ , then:

$S=(r^2/2)(\sin (a-b+c) - \sin (a-b-c) - \sin (a+b+c) + \sin (a+b-c))$

Now for the neat part where we use the angle sum being 180°. Then,

$\sin (a-b+c) = \sin(180°-2b) = \sin (2b)$

$\sin (a-b-c) = \sin(-180°+2a) = - \sin (2b)$ (watch signs!)

$\sin (a+b-c) = \sin(180°-2c) = \sin (2c)$

$\sin (a+b+c) = \sin(180°) = 0$

So we get this elegant result:

$S=(r^2/2)(\sin (2a) + \sin (2b) + \sin (2c))$

Area of Triangle inside a Circle in terms of angle and radius

2 Answers2

Linked