1

This question is about how to prove a transformation exists between two objects $A$ and $B$, $f : A \to B$. First I explain what the problem I'm having is, followed by the questions.

I am confused with how to prove isomorphism between two objects, or I guess more generally a transformation between two objects. It seems that you can create an isomorphism/transformation by definition, and there is no need for proof. But in the programming / software world, you can't just say $f : A \to B$. The function needs to be implemented. More generally (in programming), instead of custom functions you can create a data structure $D$ such that $f : \{A, D\} \to B$ or $f_D : A \to B$ to define the transformation; the generic function just uses the data structure to perform the transformation. As such, it seems there's some sort of information in that data structure that can be used somehow in a proof of the transformation. But I'm confused because mathematically the implementation / data structure stuff is left out -- you just write $f : A \to B$. So I'm wondering what is actually necessary to prove a transformation exists between two objects.

For reference, I am also ~somewhat~ thinking in terms of Homotopy Type Theory (HoTT). In that field (from my understanding), a proof of equivalence between two types is that a path exists between them. I imagine this path to be like a transformation. But in HoTT, just stating two types are equal (i.e. that a path exists) is enough. You don't have to define the algorithmic steps or anything between the two types (whereas you would if in software you actually want to perform a transformation).

So I am wondering:

  1. Given two objects $A$ and $B$, how to prove there is a transformation $f : A \to B$ that exists between them. Wondering if you have to show step by step the algorithmic transformation, or if you just have to show there is a path of some sort, or something else (that's all I can think of). I haven't been able to understand how to prove a transformation exists (keep thinking along the lines of a step-by-step algorithm to transform but not sure if that's the right track). Not sure what to do here, but I feel just stating that "there is a transformation" is not rigorous enough. I would like the transformation to be shown and have the rigor of a proof.
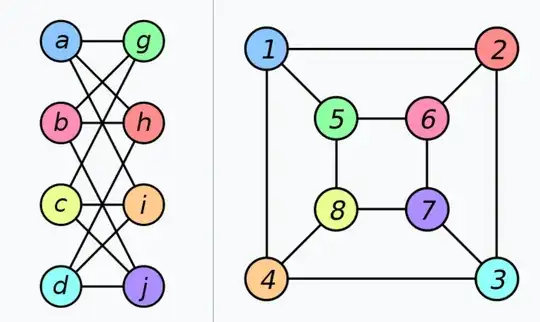
  2. If there is a transformation between two objects (like the coffee cup $\to$ donut example), wondering if that is considered an isomorphism, or if not, then it is just a general transformation / equivalence. Not sure the terminology there. Hoping to understand how to distinguish between transformations and isomorphisms. Not clear to me how they are different in these examples, given that there is a bijection. In programming, the two structures might be two different graphs, with a bijection between them (but the data associated to each vertex might be different between the two graphs), so maybe this has something to do with graph isomorphism.

I'm just wondering at a high level how to do this, not necessarily a specific proof if it involves too much. Basically, what I need to show in order to be able to say "we have a proof of the transformation between $A$ and $B$" or that "$B$ is proven to be derived from $A$". I am wondering if there is a way to have the rigor of proofs in this setting.

By "object" I mean any sort of mathematical structure, but specifically in this example I am thinking in terms of graphs. More generally, I am thinking in terms of the 3 images below (topology transformation, path transformation, and graph transformation), which all seem similar to me in that there are two points/graphs/paths/objects/structures $A$ and $B$, and a transformation between them.

enter image description here enter image description here enter image description here

Lance
  • 3,698

1 Answers1

2

I'll try a high level rather general answer to a very (too) general question.

You ask

Given two objects $A$ and $B$, how to prove there is a transformation $f:A→B$ that exists between them.

The only answer that makes sense to me is that you use what you know about the particular objects $A$ and $B$ in the particular problem. Usually the "transformation" is meant to preserve properties shared by the objects. So, for example, if you know enough elementary abstract algebra you can show that any two cyclic groups of the same order must be isomorphic. You can even count, and write down, all the possible isomorphisms. If you know enough about the definition of cardinality you can show that there are countably many rationals but uncountably many reals.

Then you ask about

how to distinguish between transformations and isomorphisms.

In the context of your question, "transformation" seems to be a rough synonym for "function", sometimes implicitly a bijection. Whether or not a bijection is an isomorphism depends on the structural properties of the objects. For example, any of the usual bijections between the integers and the rationals is an isomorphism when you are thinking of those objects as sets, but can't be an isomorphism when you are thinking of them as additive groups, since one is cyclic and the other not.

Two graphs are isomorphic if there's a bijection between the vertex sets that preserves the pairs of vertices that determine edges. (That definition allows for multiple edges and loops.) But if the graphs are directed graphs you will want to demand more before you call such a bijection an isomorphism. Whether you need to preserve "the data associated to each vertex" determines whether you call any particular bijection an isomorphism in your application.

My response to

what I need to show in order to be able to say "we have a proof of the transformation between $A$ and $B$" or that "$B$ is proven to be derived from $A$". I am wondering if there is a way to have the rigor of proofs in this setting.

is that the level of proof required depends on the level of precision with which you have specified $A$ and $B$. The wikipedia animation converting a cup to a donut is rigorous if you consider the pictures of the cup and the donut as rigorous definitions of those objects. If you define them as differentiable manifolds with specific atlases of charts then you have to provide the actual functions that implement the mapping. Of course that's in effect what the programmer did to make the animation. He or she probably did not formally verify the differentiability.

Possibly helpful: What is an Homomorphism/Isomorphism "Saying"?

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
  • Hmm, thank you for this it helps. From what I am getting then it sounds like proving isomorphism depends on your knowledge of the system (which makes it feel arbitrary). If graph $A$ has 20 nodes and graph $B$ has 10 nodes, but each node is a "super node" combining 2 nodes from $A$, then I can in my head reason they are isomorphic. But the vertices are different. So it seems like these requirements for proof are based on arbitrary definitions. Which keeps me confused. – Lance May 25 '18 at 14:47
  • "The wikipedia animation converting a cup to a donut is rigorous if you consider the pictures of the cup and the donut as rigorous definitions of those objects." This helps. – Lance May 25 '18 at 14:50
  • 1
    When you start talking about "super nodes" you are changing the definition of "graph", so implicitly changing the definition of isomorphism. In OOP terms, you have two different classes. Perhaps it's convenient when one inherits from the other. The definition of isomorphism (perhaps but not necessarily overriding an equals method) will have to change. – Ethan Bolker May 25 '18 at 14:53
  • You have asked an interesting question. I tell my students that every interesting question has the same answer: "it depends". So that should not bother you or make you unhappy. If you can just calculate the answer or look it up the question isn't interesting. – Ethan Bolker May 25 '18 at 14:57