19

Problem

Prove or disprove that $2^{\frac{\pi}{2}}$ is an irrational number.

My Try

According to our mathematical intuition, we may want to apply Gelfond–Schneider theorem, which states that

if $\alpha,\beta$ are two algebraic numbers, where $\alpha$ dose not equal $0$ or $1$ and $\beta$ is not a rational number, then $\alpha^\beta$ is a transcendental number.

But in fact, it can't work here, because $\beta=\dfrac{\pi}{2}$ here is not an algebraic number at all, which doesn't satisfy the premise of the theorem.

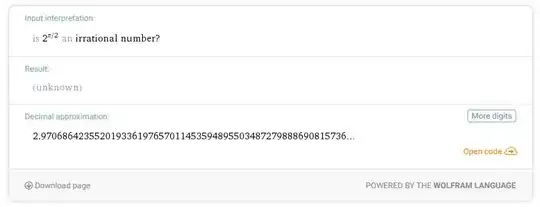
Besides, I have tested this on WolframAlpha. It outputs the consequence as follows

enter image description here

Now, how to go on?

Community
  • 1
mengdie1982
  • 13,840
  • 1
  • 14
  • 39
  • What is the source of this problem? There are tricks that can sometimes be applied to problems like this (e.g. we can prove that irrationality of $e^\pi$), but I don't see anything that would clearly apply in this instance... – Steven Stadnicki May 25 '18 at 01:16
  • 2
    Oh, this problem doesn't need any particular source, Maybe, it naturally comes from our mathematical thinking? – mengdie1982 May 25 '18 at 01:20
  • 7
    Related: https://proofwiki.org/wiki/Is_2_to_the_power_of_Pi_Rational%3F – Michael May 25 '18 at 01:23
  • 2
    @mengdie1982 The way the question was phrased when I initially wrote my reply was 'prove that $2^{\pi/2}$ is irrational', suggesting that you were being asked to find a proof; that, and the seemingly-arbitrary choice of $\pi/2$ rather than $\pi$ in the exponent, are why I asked to the source, because AFAIK (and as Michael's link suggests) the problem is open. If you were inquiring about the status, then I would suggest a title along the lines of 'Is it known whether $2^{\pi/2}$ is rational or not?' – Steven Stadnicki May 25 '18 at 01:31
  • @Michael You mean this is a pendent problem? But the rationality or irrationality of $2^{\pi}$ seems not to imply anything on my problem. – mengdie1982 May 25 '18 at 01:31
  • @StevenStadnicki yes,sir... I have revised my title, only because I'm not sure that it's really an irrational number. – mengdie1982 May 25 '18 at 01:37
  • @mengdie1982: Surely if $2^\pi$ is irrational then so is $\sqrt{2^\pi}=2^{\pi/2}$. – hmakholm left over Monica May 25 '18 at 02:00
  • In a similar spirit @HenningMakholm if $2^{\pi/2}$ was known to be rational then $2^{\pi}$ would be rational. So, if it is known what $2^{\pi/2} $ is then it must be irrational. – clark May 25 '18 at 02:19
  • If it were rational, we would have $\pi=\frac{2(\ln p - \ln q)}{\ln 2}$. Maybe there are some theorems that $\pi$ cannot have this form? – SK19 May 25 '18 at 02:37
  • @SK19 It is unknown if $2^{\pi}$ is irrational or rational. – clark May 25 '18 at 02:44
  • @clark Yes, people have noted. I don't know about you, but just because something is unproven doesn't mean I can't try. – SK19 May 25 '18 at 03:07
  • 1
    @SK19 bless your heart brother, just wanted to make sure in case you missed it. Side note: I have spent a lot of time, in the past, trying to solve Goldbach's conjecture, so I can relate. – clark May 25 '18 at 03:12
  • 1
    @SK19 You're welcome to try, but this is not the kind of problem that will get a one-line (or even one-page) proof. – Robert Israel May 25 '18 at 04:35
  • Taking $2^\pi = e^{\pi\ln(2)}$, i.e. three transcendental numbers. Are there any theorems on this? For example instinctively, $\pi\ln(2)$ seems like it might also be transcendental (it is certainly irrational if that is enough). I should point out that I am not really well equipped to tackle this. Just tossing ideas around. – Jepsilon May 25 '18 at 04:37
  • 2
    @Jepsilon: Unfortunately that's the opposite knowledge of what would be useful. If $\pi \ln(2)$ happened to be rational (or even algebraic) then the Lindemann-Weierstrass theorem would tell us that $2^\pi$ is transcendental, but if $\pi\ln(2)$ is transcendental, we're no further. Do you know that $\pi\ln(2)$ is irrational, though? It's not obvious to me. (Multiplying the Leibniz series and the alternating harmonic series might give something that's nice enough to work with. But since they're only conditionally convergent, multiplying term by term is not automatically valid). – hmakholm left over Monica May 25 '18 at 11:20
  • For $\pi \ln(2)$ I reasoned that since transcendental numbers are defined to be such that you cannot get to a rational using any finite number of algebraic operations, then them being transcendental would not set the condition for their product to be rational. Is this wrong? – Jepsilon May 25 '18 at 13:36
  • 1
    @Jepsilon that's not an easy question. For instance it is not known if $\pi\cdot e$ or $\pi+e$ are irrational or not. How, can we distinguish $\pi\cdot e$ from the case $\pi \cdot \pi^{-1}$? – clark May 25 '18 at 17:04
  • @clark oh ok I see what you mean now – Jepsilon May 26 '18 at 16:44

1 Answers1

0

As noted in the comment section, the irrationality of $2^\pi$ is unknown, so is that of $2^{\pi/2}$.

Klangen
  • 5,075