Simple trig integration

Question

I have nearly solved this question but I'm getting a different answer when substituting limits:

$∫_0^2 \left[\sin⁡(2x)+\sec^2 (\frac{x}{2})\right]\,dx $

integrated to: $-\frac{1}{2}\cos(2x)+2\tan(\frac{x}{2})+c$

substituting limits:

($-\frac{1}{2}\cos(4)+2\tan(1))-(-\frac{1}{2}\cos(0)+2\tan(0))+c$

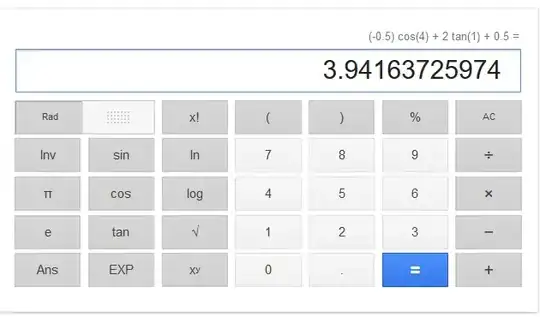
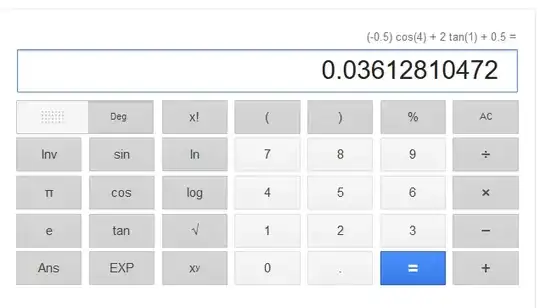
simplify: $-\frac{1}{2}\cos(4)+2\tan(1)+\frac{1}{2}$

For me this evaluates to $0.036128...$, but the solution is actually $3.94163$...

Is there something obvious I'm missing?

When you're doing a definite integral, the constant of integration cancels out. Also, is your calculator in the right mode? Degrees versus radians? — Adrian Keister, May 22 '18 at 17:32
Thanks. So is 0.036128 degrees equally correct? Also, does that mean the limits should be stated in radians? How would one know whether an integral should be reported in radians or degrees? — Paddington, May 23 '18 at 11:52
Thanks again. I just found this guide which explains it nicely. — Paddington, May 23 '18 at 12:01

score 5 · Answer 1 · answered May 22 '18 at 17:35

5

Did you use Degrees or radians while calculating it, because it is correct for radians.

radians

degrees

answered May 22 '18 at 17:35

The Integrator

1 Answers1