5

I photographed a rectangular shape, but:

  • the camera angle is not perfect
  • the image is possibly rotated.

Given the coordinates of 8 points $ A_1 (x_1, y_1), ..., A_8 (x_8, y_8)$, how to transform the input coordinates into perfectly rectangular output coordinates?

enter image description here

Note:

1) Additional information: the deskewed rectangle has a width $W = 21\ cm$ and a height $H = 29.7\ cm$. Also $A_1 A_2 A_4 A_3$ is a square of 1 cm x 1 cm, and $A_5 A_6 A_8 A_7$ too.

2) The problem will probably have multiple solutions, up to rotations of 90 or 180 degrees

3) It's probably possible with only 6 points (or even less?) but I'd like to make use of all the 8 points to improve quality (it's an overdetermined problem, so using least-squares could probably help, but I don't know how to do it in this context)

Basj
  • 1,671
  • 1
  • 22
  • 44
  • Even if you fix the "target" rectangle of assigned height and width, the mapping is not unique because of the rotational symmetry of the rectangle, e.g. it could be rotated through an angle $\pi$ without change. – hardmath May 20 '18 at 18:29
  • Already answered at https://math.stackexchange.com/q/296794/1257 – brainjam May 20 '18 at 18:37
  • @brainjam it's related but not exactly the same (see my last remark in question) – Basj May 20 '18 at 18:41
  • Sorry, I didn't notice that you had 8 source points. Generally 4 is sufficient, along with 4 target points. Since you are posing an overdetermined problem you probably want something like a least squares solution, like https://pdfs.semanticscholar.org/ea51/33a54d8134765d9479ae62b538e2813f5c3d.pdf The problem is that you don't know what the target points would be that correspond to any of the source points other than $(x_1,y_1)$ and $(x_8,y_8)$. – brainjam May 21 '18 at 15:37
  • @brainjam Yes, it's overdetermined and I was also thinking about least squares, but not sure how to do it in this context. See my updated Note 1 in the question for more informations: I do know the target points for all points $A_i$, for $i \in {1, 2, ..., 8}$. – Basj May 21 '18 at 15:57
  • To move forward you should justify whether using 8 points instead of 4 is really worth the significant extra effort. And if you still think 8 points is a good idea you should explain where the existing least squares solutions literature is not helping. – brainjam May 21 '18 at 18:30
  • @brainjam which 4 points? I only have points at the top left corner and points at the bottom right of the page, but no point at the top right for example. – Basj May 21 '18 at 19:00
  • I had assumed you could easily get the top right point. But if not, any 4 of the 8 points should do. In fact, if you give me 4 points (and their targets) I can run them through WolframAlpha for you to get a transform. – brainjam May 21 '18 at 21:15
  • Let us continue this discussion in chat. – Basj May 21 '18 at 21:20

3 Answers3

7

1) Only four points (like four corners of a sheet of paper) are enough to do the deskewing, the transform is known as a "homography" (as stated in another answer). See also this answer about these transformations. Here is how to do it on an image with only a few lines of Python + OpenCV:

enter image description here

2) When we want to use 8 points to do it, the problem is overdetermined, and we want to find the optimal solution by minimising an error (least-squares style). It's exactly what findHomography from the library OpenCV does (see remarks there about minimization of error). Here is how to do it with Python + OpenCV:

import cv2 
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('IMG_20180522_211242_2.jpg')
pts1 = np.float32([[58,642],[147,627],[83,733],[168,716],[2320,2654],[2291,2566],[2238,2675],[2211,2588]])
pts2 = np.float32([[50,50],[150,50],[50,150],[150,150],[2100-50, 2970-50],[2100-50,2970-150],[2100-150,2970-50],[2100-150,2970-150]])
size = (2100,2970)

M, mask = cv2.findHomography(pts1,pts2)
dst = cv2.warpPerspective(img,M,size)

plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

enter image description here

Note: I now realize this is a programming+math question/answer (if so, feel free to migrate it to StackOverflow), or maybe half math/half programming, and then another more math-oriented-answer is welcome.

Basj
  • 1,671
  • 1
  • 22
  • 44
3

QuadrilateralGrid[q_List, nx_, ny_] := Module[{u, i, grf, graphics = {}}, For[i = 1, i <= nx, i++, u = i/nx; AppendTo[graphics, ParametricPlot[(q[[1]] u + q[[2]] (1 - u)) v + (q[[4]] u + q[[3]] (1 - u)) (1 - v), {v, 0, 1}]]]; For[i = 1, i <= ny, i++, u = i/ny; AppendTo[graphics, ParametricPlot[(q[[2]] u + q[[3]] (1 - u)) v + (q[[1]] u + q[[4]] (1 - u)) (1 - v), {v, 0, 1}]]]; AppendTo[graphics, ListLinePlot[{q[[1]], q[[2]], q[[3]], q[[4]], q[[1]]}, PlotStyle -> Red]]; Return[graphics] ]

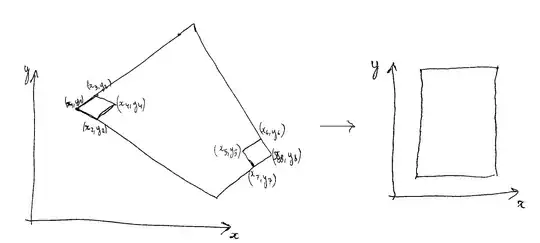
QuadrilateralCoords[q_List, p_List] := Module[{coords = {}, i, x, y, sol, c0 = q[[3]], c1 = q[[4]] - q[[3]], c2 = q[[2]] - q[[3]], c3 = q[[1]] - q[[4]] - q[[2]] + q[[3]], s1, s2, s0}, For[i = 1, i <= Length[p], i++, sol = Quiet[ Solve[Thread[c0 + x c1 + y c2 + x y c3 == p[[i]]], {x, y}]]; If[Length[sol] < 2, s0 = ({x, y} /. sol)[[1]], s1 = {x, y} /. sol[[1]]; s2 = {x, y} /. sol[[2]]; s0 = s2; If[s1[[1]] > 0 && s1[[1]] < 1 && s1[[2]] > 0 && s1[[2]] < 1, s0 = s1]]; AppendTo[coords, s0] ]; Return[coords] ] QuadrilateralPlotPoints[q_List, coords_] := Module[{graphics = {}, nc = Length[coords], i, u, v, p1, p2, p0, , diag1 = Norm[q[[1]] - q[[3]]], diag2 = Norm[q[[2]] - q[[4]]], diag, rad}, diag = Max[diag1, diag2]; rad = 0.008*diag; For[i = 1, i <= nc, i++, u = coords[[i, 1]]; v = coords[[i, 2]]; p1 = q[[1]] u + q[[2]] (1 - u); p2 = q[[4]] u + q[[3]] (1 - u); p0 = p1 v + p2 (1 - v); AppendTo[graphics, Graphics[{Red, Disk[p0, rad]}]]]; AppendTo[graphics, ListLinePlot[{q[[1]], q[[2]], q[[3]], q[[4]], q[[1]]}, PlotStyle -> Red]]; Return[graphics] ] 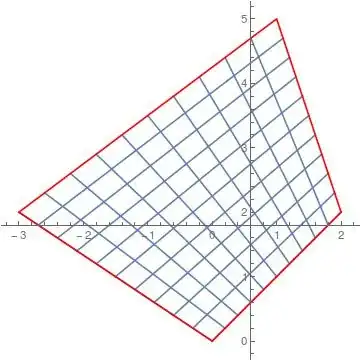quadrilateral = {{0, 0}, {2, 2}, {1, 5}, {-3, 2}}; base = {{0, 0}, {2, 0}, {2, 3}, {0, 3}}; Show[QuadrilateralGrid[quadrilateral, 10, 10], PlotRange -> All ] Show[QuadrilateralGrid[base, 10, 10], PlotRange -> All ] 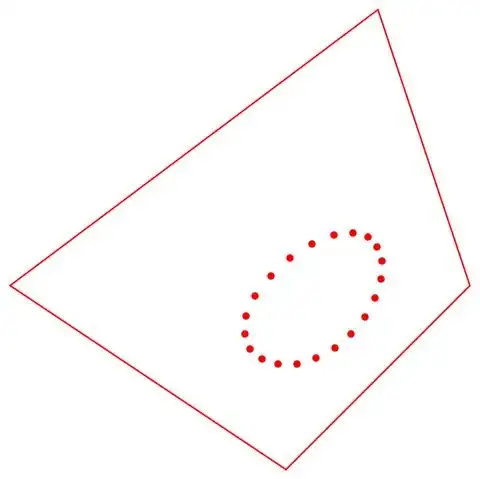enter image description here

enter image description here

basepoints = Table[{0.5 Cos[t] + 1, 0.5 Sin[t] + 1}, {t, 0, 2 Pi, 0.3}]; coordsbase = QuadrilateralCoords[base, basepoints]; Show[QuadrilateralPlotPoints[quadrilateral, coordsbase]] Show[QuadrilateralPlotPoints[base, coordsbase]]

enter image description here

enter image description here

Cesareo
  • 33,252
1

You need to compute a projective transformation (aka homography, collineation). Details at Finding the Transform matrix from 4 projected points (with Javascript)

If you want to pursue least squares methods you might find this Mathematica answer helpful: https://mathematica.stackexchange.com/questions/9244/solve-system-of-equations-related-to-perspective-projection

brainjam
  • 8,626