How lim $h->0$ $\sin h/h$ is equal to $1$?

Question

How $\lim_{h\to 0} \sin h$ when divided by $h$ gives the value $1$ ? Does it also follows with other ratios that for example. $\lim_{h\to 0} \cos x/x = 1$

Answer 1

First of all, it is not true that $\sin(x)\over x$ is $1$. In fact, this is never true (note that $\sin(0)\over 0$ is undefined). For example:

• ${\sin(\pi)\over\pi}=0$.

• ${\sin({\pi\over 3})\over {\pi\over 3}}={{\sqrt{3}\over 2}\over{\pi\over 3}}={3\sqrt{3}\over 2\pi}$.

• And so on.

What is true is that $$\lim_{h\rightarrow 0}{\sin(h)\over h}=1,$$ but this doesn't say that there is a specific value of $h$ such that ${\sin(h)\over h}=1$; rather, it says intuitively that by picking $h$ really really close to $0$ we can make $\sin(h)\over h$ really really close to $1$.

The precise definition of the limit is a bit more complicated: when we say $$\lim_{h\rightarrow 0}{\sin(h)\over h}=1,$$ what we mean is that for any $\epsilon>0$ (the "degree of accuracy") we can guarantee that $\sin(h)\over h$ is within $\epsilon$ of $1$ just by making sure that $h$ is close enough to $0$; fully formally, that for all $\epsilon>0$ there is some $\delta>0$ such that $$0<\vert h-0\vert<\delta\implies \vert {\sin(h)\over h}-1\vert<\epsilon.$$ (There is a slight asymmetry here, namely the "$0<$" on the $\delta$-side but not on the $\epsilon$-side, but that's best ignored at first.)

---

Re: your other question, this is a specific property about $\sin$. For example, $$\lim_{h\rightarrow 0}{\cos(h)\over h}$$ is undefined (from the left it approaches $-\infty$ and from the right it approaches $+\infty$).

Answer 2

Note: The original question asked whether $\frac{\sin x}{x} =1$, not whether it's limit did as $x\to0$. This answer is directed at the former question in order to address any misconceptions but also addresses the latter.

---

It's not, but $\sin (x)/x \approx 1$ for $|x|\ll 1$ is a very common approximation in physics and engineering.

If you're familiar with the Taylor series, the explanation below is straightforward. If not, then take it for a fact that $\sin x$ can be written as an infinite sum of the form

$$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots$$

Then dividing by $x$, we have

$$\frac{\sin x}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} + \dots$$

If $|x|\ll1$, then the higher order terms will be small in comparison to $1$, which is where the approximation comes from. In the limit as $x\to0$, $\sin(x)/x\to 1$.

Answer 3

"$\frac {\sin x}{x} = 1$" is a special case.

And is not correct if we don't give it the right context.

$\lim_\limits{x\to 0}\frac {\sin x}{x} = 1$

When $x\in (-\frac {\pi}{2},\frac {\pi}{2})$

$|\sin x| \le |x| \le |\tan x|$

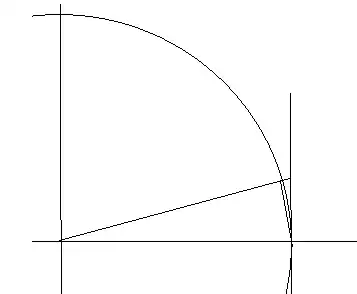
If that it not obvious, consider this figure:

The smaller triangle has area $\frac 12 \sin x$ It sits inside a section of a circle of area $\frac 12 x$ Which in turn sits inside a triangle of area $\frac 12 \tan x$

$1 \le \frac {x}{\sin x} \le \sec x\\ 1 \ge \frac {\sin x}{x} \ge \cos x$

And as $x$ approaches $0,\frac {\sin x}{x} = 1$ by the squeeze theorem.

$\lim_\limits{x\to 0}\frac {\sin x}{x} = 1$ is a property that depends on the definition of $\sin x.$ It does not generally apply to the other trig functions.

However, it is indeed true that $\lim_\limits{x\to 0}\frac {\tan x}{x} = 1$

$\lim_\limits{x\to 0}\frac {\tan x}{x} = \left(\lim_\limits{x\to 0}\frac {1}{\cos x}\right)\left(\lim_\limits{x\to 0}\frac {\sin x}{x}\right) =1$

Answer 4

One way to think about this is to recall the relationship between the trig functions and circles (in particular and wlog, the unit circle).

First, we're measuring angles by arc length subtended (i.e., in radians). The theorem comes from the fact that when the angle is very small (call it $\theta$), then $\sin\theta\approx\theta\approx\tan\theta$ (draw a diagram!). More correctly, though, what holds is that $$\sin\theta<\theta<\tan\theta$$ for $\theta<π/2$, so that we have, upon division by $\sin\theta$ and taking reciprocals, that $$\cos\theta<\sin\theta/\theta<1.$$ Now letting $\theta \to 0$, we obtain the result (a similar argument can be made from the other direction).

No, it doesn't hold for the other trig functions similarly. In particular, $$\lim_{\theta\to 0}{\cos\theta/\theta}=\infty.$$