0

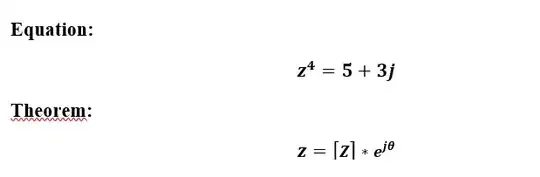
How can i find the 4 roots of the below equation by using the exponential method? enter image description here

AGR
  • 43
  • Use the theorem. Convert your complex number $5+3j$ into the form $re^{j\theta}$ where $r,\theta$ are to be found. Then finding the roots is simply a matter of taking the 4-th root and using the fact that $e^{2\pi kj}=1$ where $k\in\mathbb{Z}$. – pshmath0 May 08 '18 at 17:11

1 Answers1

0

Let $z_1 = 5+3j$

Converting to polar coordinates gives ;

$z_1 = \sqrt{34}e^{j\arctan(\frac35)}$

Now;

$z^4 = z_1(1)$

$z^4 = \sqrt{34}e^{j\arctan(\frac35)}\cdot e^{2k\pi j}$ $\quad$as $1= e^{2k\pi j}$

$z^4= \sqrt{34}e^{j\arctan(\frac35)}\cdot e^{2k\pi j}$

$z =(34)^{\frac18}e^{\frac{\arctan(\frac35)}{4}j} \cdot e^{\frac{2k\pi}4 j}$

$z = (34)^{\frac18}e^{\frac{\big(2k\pi+\arctan(\frac35)\big)}{4}j} $

So letting $k = 0,1,2,3$ gives us the 4 roots;

Which are $(34)^{\frac18}e^{\frac{\big(\arctan(\frac35)\big)}{4}j} ,(34)^{\frac18}e^{\frac{\big(2\pi+\arctan(\frac35)\big)}{4}j},(34)^{\frac18}e^{\frac{\big(4\pi+\arctan(\frac35)\big)}{4}j},(34)^{\frac18}e^{\frac{\big(6\pi+\arctan(\frac35)\big)}{4}j}$

The Integrator
  • 3,200