2

Consider the quadratic equation $x^2 + Bx + C = 0$ where $B$ and $C$ are independent and have uniform distributions on $[−n, n]$. Find the probability that the equation has real roots.

I know that $x\in\mathbb{R}$ iff $B^2/4\ge C.$I'm looking for $P(B^2/4\ge C).$ So basically, I need to draw the region $C\leq B^2/4$ and compute the area. The area inside of the square $[-n,n]\times[-n,n]$ and below the function is given by

$$A_N=\int_{-n}^{n}\frac{B^2}{4} \ dB + 2n^2= \frac{n^3}{6}+2n^2,$$

and the total area of the square is $A_T=(2n)^2=4n^2$ so

$$P(B^2/4 \geq C)=\frac{A_N}{A_T}=\frac{\frac{n^3}{6}+2n^2}{4n^2}=\frac{n}{24}+\frac{1}{2}.$$

The answer is $1/2+n/24$ for $n\le4$ and $1-2/(3\sqrt{n})$ for $n\ge 4.$

Why does one need to splitt it into cases like this?

EDIT:

I Editet my question since I figured out the first part of my problem. The question above remains.

Parseval
  • 6,413
  • 1
    Note that your answer is $>1$ when $n>12$. This is not possible – Martín Vacas Vignolo May 06 '18 at 16:54
  • Draw a picture for say n=1 and n=5 and shade the region of the event. – Batman May 06 '18 at 16:55
  • @MartínVacasVignolo - Ok so then the point at which the answer should change should be 12 and not 4? – Parseval May 06 '18 at 16:59
  • @Batman, I did. Only thing that happened was that the region increased in size. – Parseval May 06 '18 at 16:59
  • @Parseval no. My point was that your answer is not valid. The problem is that the parabola can intercept the vertical sides of the square ($n\leq 4$) or the horizontal (up) side of the square ($n>4$) – Martín Vacas Vignolo May 06 '18 at 17:06
  • @Parseval and then the integral $\int_{-n}^n$ is wrong – Martín Vacas Vignolo May 06 '18 at 17:07
  • @MartínVacasVignolo - Ok I understand why things change when $n\geq 4.$ But How would I arrive at the correct answer by setting upp a proper integral? – Parseval May 06 '18 at 17:18
  • @MartínVacasVignolo - I suppose it just comes with drawing and looking att the figure for different values of $n$. But then my integral is correct if $n\leq 4$. I suppose I just have to set up 2 different integrals then. – Parseval May 06 '18 at 17:22
  • Yes, you have 2 cases. When $n>4$ consider the values of $x$ such that $x^2/4=n$ (ie, the intersections of parabola with the horizontal side). The area will be $\int_{x_1}^{x_2}x^2/4dx$ + 2 area rectangule (with sides $n$ and $n-x_i$ – Martín Vacas Vignolo May 06 '18 at 17:26
  • @MartínVacasVignolo - Yes I got it. for $n\geq4$ the answer becomes $$\int_{-2\sqrt{n}}^{2\sqrt{n}}\frac{B^2}{4} \ dB+2n\cdot (n-2\sqrt{n})+2n^2=1-\frac{2}{3\sqrt{n}}.$$ – Parseval May 06 '18 at 17:29
  • Similar Q&A – BruceET May 06 '18 at 17:51
  • Same question asked a few days back:https://math.stackexchange.com/questions/2758675/the-probability-that-the-quadratic-equation-has-real-roots. – StubbornAtom May 06 '18 at 18:00

1 Answers1

2

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$

Hereafter I'll use Iverson Bracket which is a convenient 'tool' to handle constraints. Namely, $\ds{\bracks{P}}$ is equal to $\ds{\color{red}{ONE}}$ whenever $\ds{P}$ proposition is $\ds{\large\texttt{true}}$ and $\ds{\color{red}{ZERO}}$ otherwise.

\begin{align} &\bbox[10px,#ffd]{\ds{{1 \over 2n}\int_{-n}^{n}{1 \over 2n} \int_{-n}^{n}\bracks{B^{2} - 4C \geq 0}\dd B\,\dd C}} = {1 \over 2n^{2}}\int_{0}^{n} \int_{-n}^{n}\bracks{C \leq {B^{2} \over 4}}\dd C\,\dd B \\[5mm] & = {1 \over 2n^{2}}\int_{0}^{n} \int_{0}^{n}\braces{\bracks{C \leq {B^{2} \over 4}} + \bracks{-C \leq {B^{2} \over 4}}}\dd C\,\dd B \\[5mm] & = {1 \over 2n^{2}}\int_{0}^{n} \braces{\bracks{{B^{2} \over 4} < n}\int_{0}^{B^{2}/4}\dd C + \bracks{{B^{2} \over 4} \geq n}\int_{0}^{n}\dd C + n}\dd B \\[5mm] & = {1 \over 2n^{2}}\int_{0}^{n} \braces{\bracks{B < 2\root{n}}{B^{2} \over 4} + \bracks{B \geq 2\root{n}}n}\dd B + {1 \over 2} \\[5mm] & = {1 \over 8n^{2}}\int_{0}^{n}\bracks{B < 2\root{n}}B^{2}\,\dd B + {1 \over 2n}\int_{0}^{n}\bracks{B \geq 2\root{n}}\,\dd B + {1 \over 2} \\[1cm] & = {\bracks{2\root{n} \leq n} \over 8n^{2}}\int_{0}^{2\root{n}}B^{2}\,\dd B + {\bracks{2\root{n} > n} \over 8n^{2}}\int_{0}^{n}B^{2}\,\dd B \\[2mm] & + {\bracks{2\root{n} \leq n} \over 2n}\int_{2\root{n}}^{n}\,\dd B + {1 \over 2} \\[1cm] & = {\bracks{n \geq 4} \over 3\root{n}} + \bracks{n < 4}\,{n \over 24} + \bracks{n \geq 4}\,{n - 2\root{n} \over 2n} + {1 \over 2} \\[5mm] & = {1 \over 2} + \bracks{n < 4}{n \over 24} + \bracks{n \geq 4}\pars{{1 \over 2} - {2 \over 3\root{n}}} \\[5mm] & = \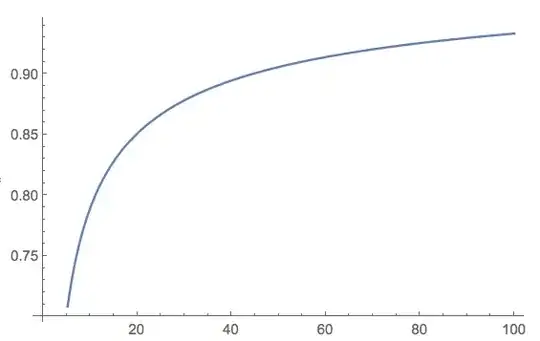bbx{\bracks{n < 4}\pars{{1 \over 2} + {n \over 24}} + \bracks{n \geq 4}\pars{1 - {2 \over 3\root{n}}}} \end{align}

enter image description here

Felix Marin
  • 89,464
  • I seriously have no idea how you can do calculations with those inequalities in the square brackets, but I'm giving you the accepted answer since you took the time writing this. – Parseval May 06 '18 at 22:26
  • 1
    @Parseval Thanks. $\displaystyle\left[\cdots\right]$ is an $\texttt{Iverson Bracket}$. I just added a brief explanation at the answer top. – Felix Marin May 06 '18 at 22:34