Why is $\cos135^{\circ}$ negative when length is always positive?

Question

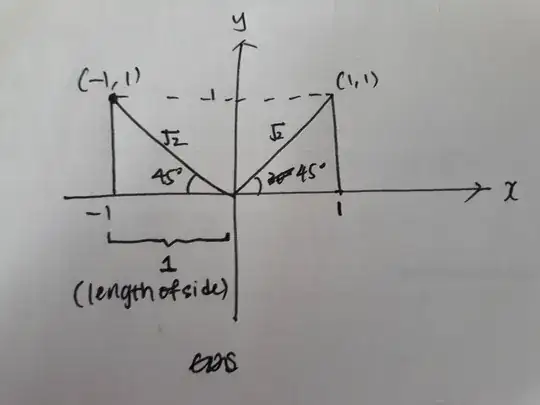
Consider the following diagram.

I am told that $\cos 45^{\circ}$ = $\frac{1}{\sqrt 2}$. I understand this.

I am next told taught that $\cos 135^{\circ}$ = $\cos 45^{\circ}$ in 2nd quadrant. And finding $\cos 45^{\circ}$ in 2nd quadrant means $\frac{-1}{\sqrt 2}$.

I am puzzled - aren't we concerned about the actual length of the triangle? The magnitude so to speak. $-1$ is the x-coordinate, telling us where it falls on the xy plane. Why are we not just taking the length i.e. $\cos 135^{\circ} =\frac{1}{\sqrt 2}$.

I know the calculator gives different values, but I'd like to understand this.

Answer 1

I’ll take a different tack from the other answerers, and just point out that the wonderful Law of Cosines, $$c^2=a^2+b^2-2ab\cos C\,,$$ where $a,b,c$ are the sides of any triangle, and $C$ is the angle opposite $c$, is only true for obtuse $C\,$ if $\cos C<0$.

Try it: build a triangle with sides $3$, $5$, and $7$, and measure the obtuse angle: you’ll find that it’s $120^\circ$, whose cosine according to the unit circle is $-\frac12$. And that fits perfectly into the Law of Cosines with $a=3$, $b=5$, $c=7$ and $\cos120^\circ=-\frac12$.

Answer 2

The cosine function is not defined, for all angles, simply in terms of lengths. That definition works for first quadrant angles, but to continue the function into the other quadrants, what actually works is to use $x$- and $y$-coordinates, which can be positive or negative, instead of just lengths, which can only be positive.

The reason for doing it this way is that all of the formulas continue to work, using the definition that allows for negatives, whereas if we kept everything positive, many formulas would either fail or become much more complicated.

When presented with more than one possible definition, we choose the one that leads to the simplest, most elegant mathematics.

Answer 3

The conventional definition in triangles requires the angle to be 0-90 degree. 135 > 90 such that the traditional way is not applicable. In the axes that you shown, you can simply see that the x axis is negative, which explains the negativity in the result.

Answer 4

In your definition, you are actually taking the absolute value of $\sin x$ and $\cos x$. However, if you let them be the new definition for sine and cosine functions, you will immediately notice that they are not differentiable at $x=k\pi$ and $x=(k+\frac{1}{2})\pi$, correspondingly. That's a huge flaw.

The sine and cosine functions we use are smooth(infinitely differentiable) in $\mathbb R$, as you will learn in calculus. That enables us to express them in series representation.

Answer 5

What you are showing in the graph, is still $\cos(45)$ not $\cos (135)$

It is more practical if you work with the unit circle centered at the origin.

Then if point $P$ on the circle is such that $OP$ makes an an angle $\theta$ with the positive direction of the x-axis, the $x$ coordinate of the point $P$ is $\cos(\theta)$

Thus for $\theta = 135$, $\cos(\theta)$ is negative.

Answer 6

The cosine function is periodic and oscillates between -1 and 1. It is more appropriate to think in terms of radians than degrees, by the way, but I'll stick to degrees here. Nonetheless, once you know what values cosine takes between $0^{\circ}$ and $360^{\circ}$, for example, you then essentially know the value of any other angle. Moreover, you really just need to know what values cosine and sine take in the first quadrant. Here, they are positive, because you are calculating/working with lengths of the triangle. However, for other angles typically you need an adjustment for the sign. The diagram/technique is really just a tool to help you figure out what sign to attach to the value.

Via the double angle formula: \begin{equation*} \cos(A+B)=\cos A\cos B-\sin A\sin B \end{equation*}and therefore, \begin{align*} \cos(135^{\circ})&=\cos (90^{\circ}+45^{\circ})\\ &=\cos (90^{\circ})\cos (45^{\circ})-\sin (90^{\circ})\sin(45^{\circ})\\ &=-\sin(45^{\circ})\\ &=-\frac{1}{\sqrt{2}} \end{align*}because you already know what the cosine and sine of $45^{\circ}$ and $90^{\circ}$ are.

Answer 7

In the first quadrant $x>0, y>0, r=\sqrt{x^2+y^2}>0$ always

In the second quadrant $x<0, y>0, r= \sqrt{x^2+y^2}>0$ always

So by the definition of cosine of an angle in second quadrant $x/r$ is negative.

Answer 8

In addition to a lot of great answers here already, it's really nice to think of trigonometric functions as how we can interpret them on the unit circle. Namely, we use $\cos(x)$ to denote the $x$ coordinate of a point that started at $(1,0)$ and moved $x$ radians (or in your case, degrees) counter-clockwise. Same with $\sin(x)$ but this is the $y$ coordinate.

This corresponds to why if you plot $(\cos(t),\sin(t))$ as you let $t$ range from $0$ to $2\pi$, you get the unit circle.

So going off this idea of thinking of $\cos(x)$ as the x-coordinate and $\sin(x)$ is the $y$ coordinate, it's intuitive to understand $\cos(135^{\circ})$ as starting at $(1,0)$ on the unit circle, going $135^{\circ}$ counter-clockwise, and looking at the $x$-coordinate. You'll land at precisely $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$, which corresponds exactly to $(\cos(135^{\circ}),\sin(135^{\circ}))$