Find coordinates of unknown point given two other points and their distances

Question

There are two known points in the coordinate plane $A(x_1,y_1)$ and $B(x_2,y_2)$. The coordinates of point $C(x_0,y_0)$ are to be found, given that the distance between $A$ and $C$ is $a$ and distance between $B$ and $C$ is $b$. Also the angle between the lines $AC$ and $BC$ is $\theta$. How can $x_0$ and $y_0$ be expressed in terms of the known information?

Answer 1

HINT

The point can be found as the intersection of

• circle centered in $A$ with radius $a$: $(x-x_1)^2+(y-y_1)^2=a^2$

• circle centered in $B$ with radius $b$: $(x-x_2)^2+(y-y_2)^2=b^2$

that is

• $(x_0-x_1)^2+(y_0-y_1)^2-a^2=(x_0-x_2)^2+(y_0-y_2)^2-b^2$

from here we can find a linear equation in $x_0$ and $y_0$. Then by the intersection with one of the circle we can find out the point C (we may have $0,1,2$ or infinitely many solutions).

Answer 2

You need the formulas $$a=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}$$ $$b=\sqrt{(x_2-x_0)^2+(y_2-y_0)^2}$$ and $$\tan(\theta)=\vert{\frac{m_1-m_2}{1+m_1m_2}\vert}$$

Answer 3

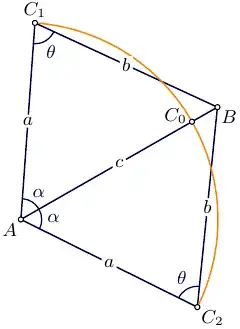
Consider points $A,B,C$ as vertices of $\triangle ABC$ with $|AC|=a$, $|BC|=b$ and $\angle ACB=\theta$.

Let $c=|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$.

Note also that $\theta$ can be found from $a,b,x_1,y_1,x_2,y_2$.

The sought point $C$ can be found by rotating the point \begin{align} C_0&=A+(B-A)\cdot\frac{a}c \end{align}

around the point $A$ by the angle $\pm\alpha$.

There is no solution, if the numbers $a,b,c$ does not form a valid triangle, otherwise there are two solutions, (unless $\sin\alpha=0$): \begin{align} x_0&= x_1+\frac{a}c\,(x_2-x_1)\cos\alpha-\frac{a}c\,(y_2-y_1)\sin\alpha ,\\ y_0&= y_1+\frac{a}c\,(y_2-y_1)\cos\alpha+\frac{a}c\,(x_2-x_1)\sin\alpha \end{align}

and

\begin{align} x_0&= x_1+\frac{a}c\,(x_2-x_1)\cos\alpha+\frac{a}c\,(y_2-y_1)\sin\alpha ,\\ y_0&= y_1+\frac{a}c\,(y_2-y_1)\cos\alpha-\frac{a}c\,(x_2-x_1)\sin\alpha , \end{align}

where \begin{align} \cos\alpha&=\frac{a^2+c^2-b^2}{2ac} ,\\ \sin\alpha&=\sqrt{1-\cos^2\alpha} . \end{align}