54

Why is the difference between these two functions a constant?

$$f(x)=\frac{2x^2-x}{x^2-x+1}$$ $$g(x)=\frac{x-2}{x^2-x+1}$$

Since the denominators are equal and the numerators differ in degree I would never have thought the difference of these functions would be a constant.

Of course I can calculate it is true: the difference is $2$, but my intuition is still completely off here. So, who can provide some intuitive explanation of what is going on here? Perhaps using a graph of some kind that shows what's special in this particular case?

Thanks!

BACKGROUND: The background of this question is that I tried to find this integral:

$$\int\frac{x dx}{(x^2-x+1)^2}$$

As a solution I found:

$$\frac{2}{3\sqrt{3}}\arctan\left(\frac{2x-1}{\sqrt{3}}\right)+\frac{2x^2-x}{3\left(x^2-x+1\right)}+C$$

Whereas my calculusbook gave as the solution:

$$\frac{2}{3\sqrt{3}}\arctan\left(\frac{2x-1}{\sqrt{3}}\right)+\frac{x-2}{3\left(x^2-x+1\right)}+C$$

I thought I made a mistake but as it turned out, their difference was constant, so both are valid solutions.

GambitSquared
  • 3,662
  • 3
    Did you actually graph both functions? That would tell a lot – imranfat May 03 '18 at 14:26
  • 1
    @Gambit What more reason would there be, other than "the algebra says it's true" – Jam May 03 '18 at 14:31
  • 2
    @imranfat https://www.desmos.com/calculator/njhbjs54rv. Looks strangely like $2$ to me. Did you actually graph both functions? – Rhys Hughes May 03 '18 at 14:31
  • 2
    @Oldboy Actually, it is. – badjohn May 03 '18 at 14:31
  • @Jam I meant to tag imranfat... my bad sorry – Rhys Hughes May 03 '18 at 14:33
  • @badjohn My bad. I did not even bother to check the simplest thing. +1 – Saša May 03 '18 at 14:38
  • @RhysHughes No, I did not. It was a mere suggestion as graphing would explain a lot. I thought it would answer itself if the OP used a graphing tool. Now that you graphed it, I clicked on the link. Now the algebra comes into play :) – imranfat May 03 '18 at 15:34
  • 28
    It doesn't matter that the numerators have different degrees. What matters is that their difference is a multiple of the denominator. –  May 03 '18 at 16:14
  • 12
    Fascinating background: at face value, I would wager that a lot of instructors would mark your answer wrong without paying much attention to how you got to it - and that most students wouldn't know to ask for a review. It is not obvious that they are both valid. I'd love to hear from educators here how would they approach this. – Euro Micelli May 04 '18 at 00:23
  • "I would never have thought the difference of these functions would be a constant." It wouldn't, if the degrees of the denominator and numerator (of the difference) were not the same (or if the numerator's difference were not divisible by the denominator). – Pedro May 04 '18 at 03:16
  • 2
    @EuroMicelli: Not an instructor, but I'd differentiate and see if I get the integrand again. – Kevin May 05 '18 at 02:12
  • @Kevin I'm afraid that verifying two expressions to be equal is not always easy. – user202729 May 05 '18 at 15:51
  • @user202729: It's much easier if you're not trying to match constant terms that might differ. – Kevin May 05 '18 at 16:17
  • 1
    Maybe it's just me, but the question as stated right now is a bit ambiguous. I'm still not sure if you're asking why you might predict that the difference is constant, or, after having reached that conclusion, why you find it to be somewhat cognitively dissonant. – kumowoon1025 May 07 '18 at 16:26

16 Answers16

83

Would you be surprised that the difference of $\dfrac{2x^2+x+1}{x^2}$ and $\dfrac{x+1}{x^2}$ is $2$?

Jared Goguen
  • 1,087
  • 23
    Not sure who is responsible for that "from review". This actually provides more of an answer to the question asked than the majority of the posts (though there are others that do better). – Paul Sinclair May 03 '18 at 18:14
  • 39
    It absolutely does provide an answer to the question, and what's more it's a good answer. It gives a simpler example of the phenomenon which the OP requests intuition for, and the intuition is easier to obtain in this simpler example. – James Martin May 03 '18 at 18:27
  • 4
    @JamesMartin: Indeed. How about: Would you be surprised that the difference of $\frac{1234}{5}$ and $\frac{234}{5}$ is $200$? – user21820 May 04 '18 at 11:26
  • 3
    Yes, this is still surprising. It is roughly equally as surprising as the difference in the original question (to me anyways). – Nick Alger May 04 '18 at 21:21
  • 2
    Yes, that's still surprising. How about actually saying why that is instead of repeating the question with slightly different values? – Nova May 05 '18 at 22:45
  • 6
    @Nova Often repeating a question with slightly different values IS the best answer. Countless times I have done this with students with great success, because it can relate a situation that the student already has intuition for to the one that they are stumped on. Maybe this answer doesn’t work for some, but that doesn’t inherently make it a bad answer. – wgrenard May 06 '18 at 07:30
  • 2
    To @NickAlger, @ Nova, and anyone else still stumped after this answer: the point is that it’s fairly easy to convince oneself that the difference of the fractions in this answer is $\frac{2x^2}{x^2}$, and then also to see that $\frac{2x^2}{x^2} = 2$. In the original example from the question, more calculation is required because the denominator is more complicated, but essentially exactly the same thing is happening. – Peter LeFanu Lumsdaine May 06 '18 at 12:18
  • Well, I'm not really "stumped" by the answer; it just doesn't provide me any intuition for why the difference should be constant. I can and did already do the same algebraic manipulations for the original question. But there is a difference between following a sequence of algebraic manipulations and believing each step, versus understanding why a result is true at a deeper level. – Nick Alger May 07 '18 at 21:44
62

It is just a bit of clever disguise. Take any polynomial $p(x)$ with leading term $a_n x^n$.

Now consider $$\frac{p(x)}{p(x)}$$ This is clearly the constant $1$ (except at zeroes of $p(x)$).

Now separate the leading term: $$\frac{a_n x^n}{p(x)} + \frac{p(x) - a_n x^n}{p(x)}$$

and re-write to create the difference:

$$\frac{a_n x^n}{p(x)} - \frac{a_n x^n - p(x)}{p(x)}$$

Obviously the same thing and hence obviously still $1$ but the first has a degree $n$ polynomial as its numerator and the second a degree $n - 1$ or less polynomial.

Similarly, you could split $p(x)$ in many other ways.

Ma0
  • 201
badjohn
  • 8,204
37

I'm not sure anyone is speaking to your observation that the two numerators have different degrees.

Let's flip this around the other way:

\begin{align*} \frac{x-2}{x^2-x+1} + 2 &= \frac{x-2}{x^2-x+1} + 2\frac{x^2-x+1}{x^2-x+1} \\ &= \frac{2x^2 -x}{x^2-x+1} \text{.} \end{align*} That is, we started with a thing having a linear numerator and added a constant to it. But when we brought the constant to have a common denominator, it picked up a degree two factor. Then the addition was forced to produce a degree two sum.

To sum up, in the context of rational functions, when you add constants, you are adding polynomials having the degree of the denominator to the polynomials in the numerators. So constants effectively have "degree two in the numerator" in your example.

Eric Towers
  • 67,037
15

Look at it in reverse:

Take a polynomial fraction and add it to a constant. The result will be a polynomial fraction, with the same denominator and a different polynomial as the numerator.

Masked Man
  • 233
Cedron Dawg
  • 807
6

This belongs to a specific set of questions "you cannot really answer to your students" if you are a teacher.

The difference is $2=\frac{2(x^2-x+1)}{x^2-x+1}$. This is why this seems weird (but true). Even this seems weird: $$\frac{15}{7}-\frac{1}{7}=2$$
The numerators differ by 14 (not 2) but the denominators are equal. The best is to try and explain this to yourself why this perfectly fine.

Konstantinos Gaitanas
  • 9,115
5

Note that in general given a rational function

$$f(x)=\frac{p(x)}{q(x)}\implies g(x)=f(x)+c=\frac{p(x)+c\cdot q(x)}{q(x)}$$

and $\deg(p(x)+c\cdot q(x))\le \max\{\deg(p(x)),\deg(q(x))\}$.

user
  • 154,566
  • Why? Where is "the difference"? – Rolazaro Azeveires May 05 '18 at 05:59
  • @RolazaroAzeveires It is just a generalized way to see that two rational function can differ for a constant c even if denominators are equal and the numerators differ in degree, that's exactly the point of the OP. – user May 05 '18 at 06:44
  • Sure. But where is "the difference"? Why is the degree larger? Note that I can see them both, but I also did not needed to ask this. It is a typical poor mathematical reply: it is accurate but it says next to nothing, unless you already know the reply. IMO adding your comment to the reply would already make quite a difference. We can use a few words, for context, can't we? (don't take me wrong, yours is not a specially bad answer, quite a large number of answers are as your) – Rolazaro Azeveires May 06 '18 at 11:07
  • I think it is just a matter of preference, from my point of view this observation suffices to answer the OP completely and maybe also the upvoters have the same idea. There are many other answers here with concrete examples and discussion so the asker have a lot of points on view on that and you also are free to add your own answer according to your best interpretation. Thanks anyway for your advice and suggestions on that. Bye! – user May 06 '18 at 11:13
5

$$(2x^2-x)-(x-2)=2x^2-2x+2$$ Hence$$f(x)-g(x)=2\bigg(\frac{x^2-x+1}{x^2-x+1}\bigg)=2(1)=2$$

In effect, this pair of equations is a very specific case where the numerator and denominator end up lining up, and thus you get a constant for all values.

Rhys Hughes
  • 12,842
5

Since the denominators are equal and the numerators differ in degree I would never have thought the difference of these functions would be a constant.

When the numerators differ in degree, the difference between the numerators is a nontrivial polynomial that goes to infinity as $x\to\pm\infty$.

However, nobody says that this polynomial cannot grow at the same rate as the (equal) denominators, in which case the ratio will be bounded (and in particular possibly constant). There's nothing in your observation "the denominators are equal and the numerators differ in degree" that link the denominator to either the numerators or their difference, so you have no reason to think the difference in numerators should dominate the growth of the entire fraction.

hmakholm left over Monica
  • 286,031
  • Eactly, i already wanted to provide an answer before seeing this, when $x->\infty$ the first function tends to $2$, the second tends to $0$, which are both constants and give out a cte difference, this doesn't apply when the numerator is bigger than the denom, if the denom is 1 the difference would be diverging but once you divide it by a polynomial of order 2, things change to converge. – Abr001am May 04 '18 at 14:14
4

Maybe instead of integrating you need just differentiating.

$$\frac{df}{dx}=\frac{(2x^2-x)(2x-1)-(x^2-x+1)(4x-1)}{denom^2}\\ =\frac{x^2-4x+1}{denom^2}$$

In the other hand:

$$\frac{dg}{dx}=\frac{(x-2)(2x-1)-(x^2-x+1)}{denom^2}\\ \ =\frac{x^2-4x+1}{denom^2}=\frac{df}{dx}$$

See that both functions have same derivates, which means they differ by the same value from $x$ to $x'$ , this only means they have a same growth rate and they have same difference all along the range of x axis.

enter image description here

Abr001am
  • 746
  • This is something OP himself did. He was solving an integral and found an alternate answer $g$. Since $f$ and $g$ are solutions to the same integral, they defer by a constant just like you demonstrate here. OP is asking for an intuition why the two rational functions defer by only a constant. – Cyriac Antony May 06 '18 at 06:03
  • What do you intend to do with a primitive, why at all one think to ascend to an integral? one function may be integrated in an infinitely many ways but what's the point ? look in the op's post that he already found two functions completely different, you are missing the point. The intuition is clear, you shouldn't compare the numerator unconsiderably of the rest of the function, you should take it all into account, for example $f$ and $g$ are mutually excluding eachother in a derivate of the form $f+g$, but they are mutual-inclusive in $f/g$. Appearence is deceiving. – Abr001am May 06 '18 at 12:46
3

You can construct a similar puzzle from the (simpler) observation that

$$ \frac{x}{x+1} + \frac{1}{x+1} = 1 . $$

Translating, that's the same as $$ \frac{u-1}{u} + \frac{1}{u} = 1 $$ which isn't surprising at all.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
  • Yes, but in my example the degrees of the numerators are different, which caught me off guard – GambitSquared May 03 '18 at 14:34
  • 4
    The degrees are different in my example too. But I agree that yours is at first surprising. Note: this kind of rational function identity is useful sometimes when calculus instructors want to make up problems that look harder than they are. – Ethan Bolker May 03 '18 at 14:35
3

Another way of stating what everyone has said:

$2x^2 - x= 2(x^2-x+1) + x - 2$

$\Rightarrow 2x^2-x = x-2 \mod x^2-x+1$

gandalf61
  • 15,326
3

Because if $P\ and\ Q\ are\ polynomials$ then, $$\deg \left( P\pm Q \right)\le max\left( \deg \left( P \right),\deg \left( Q \right) \right)$$ where $deg$ is the degree of the polynomial. See this link

3

Here's another view on the problem:

Let's look at the fraction with the higher degree: $$f(x)=\frac{2x^2-x}{x^2-x+1}$$ We note that the degree of the numerator is the same as the one of the denominator.

Now whenever the numerator's degree is at least as large as the denominator's degree, we can do polynomial division. The result is a polynomial whose degree is the difference between the numerator's and the denominator's degree, and a rest whose degree is less than the denominator's degree.

Now since numerator and denominator have the same degree, the difference of the degrees is zero. But a polynomial of degree zero is a constant. And the division rest will be of lesser degree.

Let's do the polynomial division explicitly: $$ \begin{array}{llccl} &(2x^2-\ \ x) & / & (x^2-x+1) &=& 2\\ -&\underline{(2x^2-2x+2)}\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ x \ - 2 \end{array} %\begin{array}{rrrrcccl} %&(2x^2 & -x) & & / & (x^2-x+1) & = & 2\\ %-&(2x^2 & -2x & +2)\\ %\hline % & & x & -2 %\end{array} $$ You surely will recognize the rest as the numerator of $g(x)$

So, whenever you have a rational function whose numerator and denominator, after cancelling out, have the same non-zero degree, it is not only possible, but guaranteed that there exists another rational function with lesser degree in the numerator which differs from the original rational function only by a constant.

celtschk
  • 43,384
  • BTW, does anyone know how to make the horizontal line end at the end of the polynomial above? – celtschk May 04 '18 at 05:51
  • @farruhota: That first option destroys the alignment between the terms, and therefore is worse than the too-long line. That second option defeats the whole purpose of writing the polynomial division in its standard form. – celtschk May 04 '18 at 06:48
  • How about this: $\begin{array}{ll} &(2x^2-x) & / (x^2-x+1) = 2\ -&\underline{(2x^2-2x+2)}\ & x-2 \end{array}$ – farruhota May 04 '18 at 07:04
  • @farruhota: Still doesn't correctly align the terms. – celtschk May 04 '18 at 07:10
  • Oh well, the rest should be adjusted: $\begin{array}{ll} &(2x^2-\ \ x) & / (x^2-x+1) = 2\ -&\underline{(2x^2-2x+2)}\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ x \ - 2 \end{array}$ – farruhota May 04 '18 at 07:16
  • @farruhota: Yes, that works. It's far from pretty with all that manual spacing (and I'm not sure if it won't prove fragile in the long run), but I for now changed to (a slight variation of) this (keeping the original version in comments, in case this will break later). Thank you for the help. – celtschk May 04 '18 at 07:40
  • The highest-voted answers didn't mention "polynomial division" (though badjohn's answer implicitly used it), so I was considering answering along these lines myself, until I saw this. +1 – mr_e_man May 05 '18 at 03:54
2

I feel that it's only natural that intuition would fail you in cases like these. If you wrote the two functions out as $$f(x)=\frac{2\left(x^2-x+1\right)+\left(x-2\right)}{x^2-x+1}$$ $$g(x)=\frac{x-2}{x^2-x+1}$$ it would be obvious that the difference between them was 2. This is the first thing you could trip over, the degree of the numerator don't actually differ by 1, they are the same.

I guess if you made it a rule to divide whenever you have a rational function where the degree of the numerator is greater than or equal to the degree of the denominator until it isn't, you would get consistent results. (Kinda like how you learn waaay back how $\frac{13}{7}$ is an improper fraction, because it's actually bigger than a whole number, and that you should write it as $1\frac{6}{7}$. a function $f(x)=\frac{P(x)}{Q(x)}$ where the degree of $P(x)$ is greater than or equal to the degree of $Q(x)$ is called an improper rational function.)

But, and this might be another thing that's bugging you about this question, you can't just do that! (As my algebra teacher used to exclaim in exasperation.) You introduce a new constraint: $x^2-x+1\neq0$. Which isn't relevant if x is real, but does change things up a bit if it s a complex number.

You have asked for graphs, and ye shall receive.

This is probably what you get when you graph the two functions $f$ and $g$.

Real

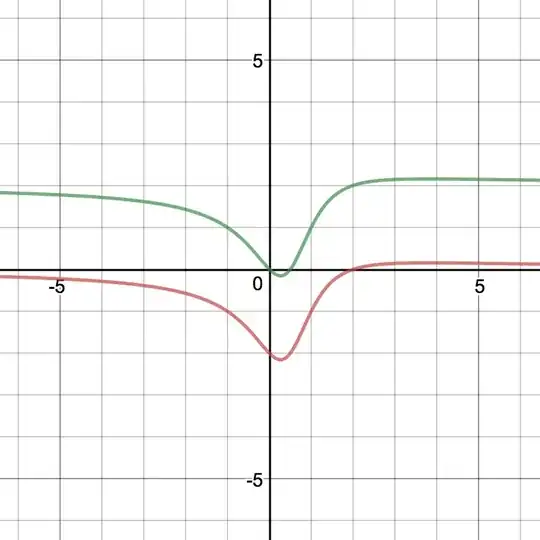
But if you allow for complex values of $x$, it can also look like this:

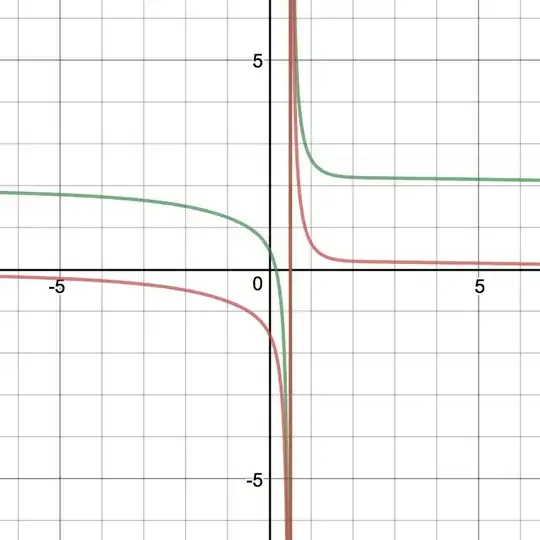
Complex

(Sans the vertical line at x=0.5, I don't know why that is happening, probably a limitation in the graphing engine on desmos.)

Not so obvious that the difference between the two is 2 in this case...

Sorry, I just realized this probably doesn't answer your question on how you can reconciliate this apparent discrepancy with your intuition, but I thought explaining why it may not be that clear-cut would help at least a little bit.

Playing with the parameters used in the graph might help further your understanding, here's a link to the interactive graph, with a little more in depth graphical interpretation of why you might doubt what you logically "know" to be true.

As for the equations I used in place of the given ones... You'll just have to trust my algebra (which you shouldn't in critical situations, but I think this is safe enough hehe). I did them on a legal pad, but I'll type them up if anyone insists.

kumowoon1025
  • 269
1

Since the denominator is the same , you subtract one numerator from the other. In this special case you find the resultant numerator is twice the denominator. Feels like that was much simpler than the rest of your background calculus.

jwovens
  • 11
  • 1
1

I shall try to explain an intuitive way to think about this.
Disclaimer: I am only developing on @gandalf61's answer.

It must be very clear to you that $11/3$ and $2/3$ defer by an integer. Why is this so? Because in the world $``$modulo 3$"$, 11 and 2 are but the same. In the same vein, we can say that in the world of $``$modulo $x^2-x+1"$, $2x^2-x$ and $x-2$ are but the same because $2x^2-x=2(x^2-x+1)+x-2$. When we are in such a world, the same polynomial may appear in different forms with different "degrees". So in a world such as the ideal generated by $x^2-x+1$ (ie $<x^2-x+1>$ ), degree is no longer retained. One's intuition may fail here because one is not familiar with such a world where degree is not so well behaved.

I hope this addresses your question. Thank you.

Cyriac Antony
  • 552