0

I am trying to find a way to approximate an ellipsoid around two points using spheres.

Take the following diagram:

enter image description here

As you can see, in my diagram (which is a cross section of the ellipsoid and the appproximating sphere)

The region of the sphere contained in between the points $P_1$ and $P_2$ is somewhat close to the actuall region on the ellipsoid.

I am looking for a method to construct such an approximating sphere that is "Good". By "Good" I mean that the method needs not be perfect, just provide a good enough approximation, even if it's analytically wrong.

EDIT:

By "around the points" I mean that the only part of the ellipsoid I actually care about is the geodesic section in between the two points. I want to approximate said geodesic with a great circle in the sphere (I know that the actual geodesic and the great circle are very different and as such this will invariably deform the surface). The goal is to try to get a good approximation of this geodesic with a sphere,

EDIT2:

The ellipsoid can be represented in any way, which includes the implicit representation and any of the possible parametrizations.

Points are represented in a standard cartesian system with three coordinates $(x,y,z)$

Makogan
  • 3,329
  • Could you clarify what do you mean by "around two points"? The figure seems to imply a "circular region" on the ellipsoid surface where the given two points are diametrically opposed. Am I reading your post correctly? – Lee David Chung Lin Apr 28 '18 at 21:52
  • @LeeDavidChungLin By around two points I mean an epsilon region around the section of the geodesic connecting the 2 points on the ellipsoid. In essence I am not trying to approximate the entire ellipsoid, justa small region around the shortest line connecting both points – Makogan Apr 28 '18 at 22:16
  • How are you parameterizing your ellipsoid? Similarly, how are you defining what the two points are? – Cedron Dawg Apr 28 '18 at 23:49
  • Implicit function or any valid parametric representation, it matters little.

    The points are 3D vectors

     – Makogan Apr 29 '18 at 00:02

1 Answers1

2

Here is a possible solution that fits these two additional conditions:

  • The approximating sphere includes the two points

  • If your ellipsoid is a sphere the approximation is exact

Let the equation of the ellipsoid be defined as:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Any point on the surface is defined as:

$$ \vec p_p = ( x_p, y_p, z_p ) $$

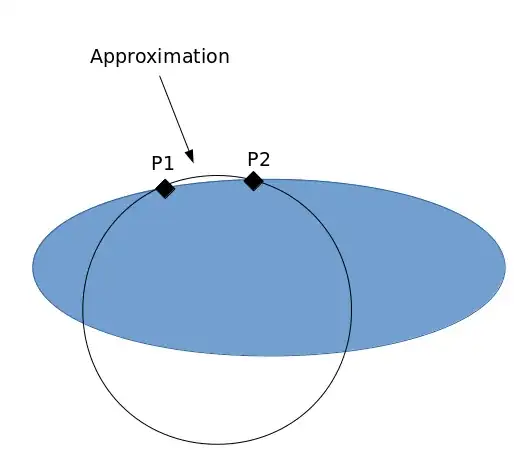
The two points in question are where $p=1$ and $p=2$.

A normal vector to the surface at any point is:

$$ \vec n_p = ( \frac{x_p}{a^2}, \frac{y_p}{a^b}, \frac{z_p}{c^2} ) $$

In order for the sphere to contain both points, its center must lay on the plane that is the perpendicular bisector of the two points. This halfway plane contains the midpoint of the two points and its normal is the difference of the two points.

$$ \vec m = \frac{ \vec p_1 + \vec p_2 }{2} $$

$$ \vec d = \vec p_1 - \vec p_2 $$

Let $ \vec h $ be any point on the plane.

$$ ( \vec h - \vec m ) \cdot \vec d = 0 $$

$$ \vec h \cdot \vec d = \vec m \cdot \vec d $$

Any line normal to the surface at point $p$ can be parameterized as:

$$ \vec g_p(t_p) = t_p \vec n_p + \vec p_p $$

The value of $t_p$ where the line intersects the halfway plane at point $ \vec q_p $ can be found:

$$ \vec q_p \cdot \vec d = ( t_p^* \vec n_p + \vec p_p ) \cdot \vec d = \vec m \cdot \vec d $$

$$ t_p^* = \frac{\vec m \cdot \vec d - \vec p_p \cdot \vec d}{\vec n_p \cdot \vec d } $$

$$ \vec q_p = t_p^* \vec n_p + \vec p_p $$

Each of the normal lines from the two points will intersect the halfway plane. For simplicity, define the center of the sphere $ \vec s $ at the midpoint of these two points.

$$ \vec s = \frac{ \vec q_1 + \vec q_2 }{2} = ( x_s, y_s, z_s ) $$

The radius is then:

$$ r = \| \vec p_1 - \vec s \| = \| \vec p_2 - \vec s \| $$

And the equation for the approximating sphere is:

$$ ( x - x_s )^2 + ( y - y_s )^2 + ( z - z_s )^2 = r^2 $$

Notice that this approach does not do any kind of fit function between the ellipsoid surface and the approximating sphere surface. If such a function were defined, it could be evaluated for spheres with centers on the halfway plane in the neighborhood of $ \vec q_1 $ amd $ \vec q_2 $. Allowing the center to move off the plane relaxes the constraint the sphere needs to contain both points.

To find your geodesic points, warp the line segment between the points to fit on the surface of the sphere.

$$ \vec v = ( t \vec d + \vec m ) - \vec s $$

$$ \vec w = r \frac{\vec v}{\|\vec v\|} + \vec s $$

Where $t$ goes from -1/2 to 1/2.

A better geodesic can probably be found by shifting the center of the sphere according to $t$, and adjusting the radius correspondingly, along the line segment:

$$ \vec s(t) = t ( \vec q_2 - \vec q_1 ) + ( \vec q_1 + \vec q_2 ) / 2 $$

I'll have to think about that. Of course, warping the line segment to fit on the ellipsoid surface would be even better.

Hope this helps.

Ced

P.S. A little post posting searching found these:

Cedron Dawg
  • 807