4

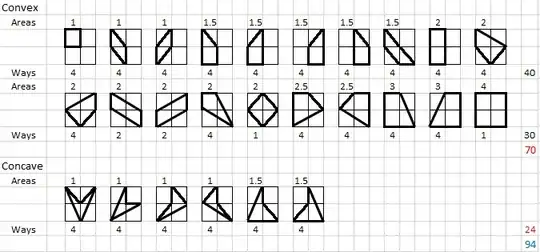
We can calculate the number of square or rectangle in a $n\cdot n$ grid.

No of squares $=1^2+2^2+3^2+.....+(n-1)^2$

No of rectangles $=1^3+2^3+3^3+.....+(n-1)^3$

So what if we want to calculate the no of all possible quadrilateral? We can choose $4$ points out of $n^2$ points.But in that case, there will be many instances where $3$ or more points will be co-linear.So these will not be a true quadrilateral. So I need to find those combinations of $3$ or more points being co-linear?

References:

How many squares are in the chessboard?

Analysis of how-many-squares and rectangles are are there on a chess board?

Community
  • 1
Dip Koley
  • 41
  • 1
    Just to worry you: there are three quadrilaterals involving the points ${(1,1), (1,3), (2,2), (3,2)}$ – Henry Apr 27 '18 at 10:09
  • 1
    The two formulas you give count the number of squares/rectangles on a chessboard, i.e., aligned with a grid, and therefor not correct here. On a $3 \times 3$ grid, there are 6 squares, i.e., four with area 1, one with area 4, but there is also a square with area 2 that is rotated 45 degrees with respect to the orientation of the grid. For larger grids additional square/rectangles are found. Also, should the quadrilaterals be convex or not? and in case of the latter, are they simple or complex (self-intersection)? – Ronald Blaak Apr 27 '18 at 16:42
  • If you are looking for sets of 4 points s.t. no 3 of them are colinear (e.g. their convex hull would be a simple quadrilateral), you can start with ${n^2 \choose 4}$ and subtract sets with 3 colinear points and sets with 4 colinear points. For those, you need to consider each possible line, not just vertical & horizontal, but there are (I think) $< n^2$ possible slopes. Probably tedious but doable. – antkam Apr 27 '18 at 22:13

2 Answers2

2

So what if we want to calculate the no of all possible quadrilateral ?

Consider $2\times 2$. Consider all possible quadrilateral shapes of specific areas and count the number of ways (by rotations and reflections). If I did not miss out any shape, here is what I got: enter image description here

farruhota
  • 31,482
  • Two minor mistakes. 8th diagram in the first line has area 1.5 in stead of 2. The 2nd and 3rd diagram in the second line only have two ways, this results then in a total of 94 different simple quadrilaterals in a $3\times3$ grid. – Ronald Blaak Apr 29 '18 at 16:39
  • RonaldBlaak, good catch, updated, thank you – farruhota Apr 29 '18 at 16:55
  • here it is given a combinatorial method: http://mathforum.org/library/drmath/view/54269.html – farruhota Apr 29 '18 at 17:00
1

This is not an answer, but the number of squares on a $n \times n$ grid is given by $n^2 (n^2 -1)/12$.

Assume $k$ (with $ 1 \leq k \leq n-1$) is the width (and height) of an arbitrary square measured along the $x$ and $y$ directions of a $n \times n$ grid. This tight ``bounding box'' can have $(n-k)^2$ different positions within that grid, whereas there are only $k$ such different squares in that box each with a different size and orientation. The total number of squares in the grid is therefor

$$\sum_{k=1}^{n-1} (n-k)^2 k = \frac{n^2(n^2-1)}{12}$$.

Ronald Blaak
  • 3,277