0

I want to diagonalize the following matrix with complex eigenvalues by real basis, but I'm not quite sure how to deal with it. Please give me some advice, thanks for help!

$\begin{bmatrix}0 & -1 & 0 & 4 \\ 1 & 0 & -4 & 0\\0 & 0 & 0 & -1\\0 & 0 & 1 & 0 \end{bmatrix}$

M.Marta
  • 9
  • How can a real matrix times a real vector possibly equal a non-real complex number times a real vector? – ancient mathematician Apr 19 '18 at 13:19
  • @ancientmathematician there is a relevant example on the first page of https://people.math.osu.edu/costin.10/5101/Eigenvalues%20p20-30.pdf It seems this is called the real Canonical Form or the Real Jordan form. I did one yesterday that had all genuine eigenvalues https://math.stackexchange.com/questions/2742114/matrix-in-canonical-form-of-an-orthogonal-transformation/2743574#2743574 This question is similar but needs that business about generalized eigenvectors. On the other hand, the final answer is all nice numbers – Will Jagy Apr 19 '18 at 18:36
  • Thanks, @WillJagy I was just objecting to a real "diagonalization" which isn't on. – ancient mathematician Apr 20 '18 at 06:40

1 Answers1

1

I finished this, I think I will revise it to agree with the example in Costin, which is the only image i could find so far that showed what I wanted. First we find the Jordan form with the complex eigenvalues; this involves generalized eigenvectors here. Next, for the two vectors for a fixed eigenvalue (here $i$) for each make a pair of real vectors out of the real and imaginary parts. Just needs care. I need to get groceries and will typeset things later, that will take some real time. Notes at COSTIN

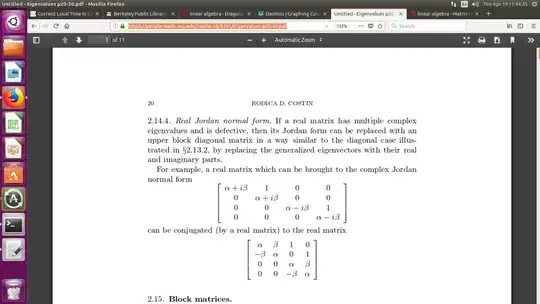
enter image description here

Here is the Jordan form $J$ and how to get there as $P^{-1}A P = J$

$$ \frac{1}{8} \left( \begin{array}{cccc} 1&i&0&0 \\ 0&0&-4i&4 \\ -i&-1&0&0 \\ 0&0&4&-4i \\ \end{array} \right) \left( \begin{array}{cccc} 0&-1&0&4 \\ 1&0&-4&0 \\ 0&0&0&-1 \\ 0&0&1&0 \\ \end{array} \right) \left( \begin{array}{cccc} 4&0&4i&0 \\ -4i&0&-4&0 \\ 0&i&0&1 \\ 0&1&0&i \\ \end{array} \right) = \left( \begin{array}{cccc} i&1&0&0 \\ 0&i&0&0 \\ 0&0&-i&1 \\ 0&0&0&-i \\ \end{array} \right) $$

Give me a bit more time, real part next. All we do is take the real and imaginary parts of the (generalized) eigenvectors that gave eigenvalue $i$ in getting $J,$ these being the first two columns on the left.

$$ \frac{1}{4} \left( \begin{array}{cccc} 1&0&0&0 \\ 0&-1&0&0 \\ 0&0&0&4 \\ 0&0&4&0 \\ \end{array} \right) \left( \begin{array}{cccc} 0&-1&0&4 \\ 1&0&-4&0 \\ 0&0&0&-1 \\ 0&0&1&0 \\ \end{array} \right) \left( \begin{array}{cccc} 4&0&0&0 \\ 0&-4&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \\ \end{array} \right) = \left( \begin{array}{cccc} 0&1&1&0 \\ -1&0&0&1 \\ 0&0&0&1 \\ 0&0&-1&0 \\ \end{array} \right) $$

Will Jagy
  • 139,541