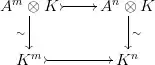In the question $A^m\hookrightarrow A^n$ implies $m\leq n$ for a ring $A\neq 0$, $A$ is a commutative ring. Is there a simpler proof for a domain, for example $\mathbb{Z}$?
Asked
Active
Viewed 69 times
2 Answers
1
Let $A$ be an integral domain and $K$ be its fractions field. Assume the existence of a injective $A$-linear map $A^m\rightarrowtail A^n$. Since $K$ is a flat $A$-module, tensoring by $K$ (over $A$) preserves injectivity, hence we get a commutative diagram of $K$-linear maps
with a $K$-linear map $K^m\rightarrowtail K^n$ of $K$-vector spaces. Note the $K$-linear isomorphism $A^n\otimes_A K\cong K^n$ which follows by induction from the canonical isomorphisms $A\otimes_A K\cong K$ and $(M\oplus N)\otimes K\cong (M\otimes K)\oplus (N\otimes K)$ explicited here. Consequently, $$m=\dim_KK^m\leq\dim_KK^n=n$$
Fabio Lucchini
- 16,054
-
Sorry, what does a "flat $A$-module" means? – Lios Apr 18 '18 at 12:24
-
Means that injectivity (or exactness) is preserved when tensored by a such module. I added a link in my answer in which you can find more details. – Fabio Lucchini Apr 18 '18 at 12:29
-
Ok perfect. I just dont know how to proof tha fact that $A^i\otimes K\simeq K^i$, but i will look for a solution. Thank you! – Lios Apr 18 '18 at 13:33
-
(if you know where I can find a proof, it would be nice!) – Lios Apr 18 '18 at 13:50
-
I added some details about the isomorphism $A^n\otimes K\cong K^n$. – Fabio Lucchini Apr 18 '18 at 20:06
1
Here is a concrete proof for $\mathbb Z$.
Every additive map $\mathbb Z^m \to \mathbb Z^n$ extends to a $\mathbb Q$-linear map $\mathbb Q^m \to \mathbb Q^n$ of $\mathbb Q$-vector spaces. If the map is injective, then its image has dimension $m$ and so $m\le n$.
When $D$ is a domain, this proof generalizes to $D$-linear maps $D^m \to D^n$ of $D$-modules, because they extend to $K$-linear maps $K^m \to K^n$ of $K$-vector spaces, where $K=Q(D)$.
lhf
- 216,483